
|
|
|
|
|
The NNSYSID toolbox is a set of MATLAB tools for neural network based identification
of nonlinear dynamic systems. The toolbox contains a number of m and MEX-files
for training and evaluation of multilayer perceptron type neural networks
within the MATLAB environment. There are functions for training ordinary
feedforward networks as well as for identification of nonlinear dynamic
systems and for time-series analysis. The toolbox requires MATLAB 4.2/MATLAB
5 with the signal processing toolbox, but it works completely independent
of the neural network and system identification toolboxes.
If you don't know what MATLAB is, you should visit The
MathWorks, Inc.
The toolbox contains:
-
Fast, robust, and easy-to-use training algorithms.
-
A number of different model structures for modelling dynamic systems.
-
Validation of trained networks.
-
Estimation of generalization ability.
-
Demonstration programs.
The toolbox has been compressed and packed into a "zip" file of approximately
0.53 Mbytes. From the matrix below you can download different versions
of the toolbox.
NOTICE that there is a special PC-version for MATLAB 4.2 As explained in
the release notes the "printf" statements works differently under Unix
and Windows 3.1. The PC version contains the toolbox with the suggested
modification for PCs. Under MATLAB5/Windows 95 this problem has been eliminated.
It appears that problems occur when trying to print the manuals on certain
printers. I have therefore used the unix-command 'ps2pdf' to convert the
manuals to pdf-format. View tutorial
section or reference
section. The manuals are included in postscript format in the zip-files
above.
MEX files
All functions in the toolbox have been implemented as M-functions. However,
to speed up some of the most time consuming functions, a few dublets have
been implemented in C and can be compiled to MEX-files. For users that
do not have access to a compiler or can't figure out how to use their compiler
I have precompiled the MEX-files for a few platforms
NOTICE:
-
Version 1.1 available from June 20, 1997. The updated toolbox contains
6 new functions and some of the old functions have been modified.
-
Pre-compiled MEX files made available as of Aug. 6
-
Help text corrected in xcorrel and title text modified in kpredict Oct.
17
-
Small bug eliminated in Matlab 5 version of the function 'obdprune',
Jul. 3, 1998.
-
Various bugs eliminated Aug. 12, 1998: 'kpredict' now works for time-series
(i.e., no exogeneous input). MEX-files now works correct for multiple weight
decay parameters when the network has been pruned. 'obsprune/obdprune/nnprune'
should now work always when called with a network which is partially pruned.
A minor bug eliminated from 'obsprune' to stabilize the function.
-
A bug was eliminated from the Matlab 4.2 version of 'obsprune' Jan.
8, 1999. The bug was due to an incompability between Matlab 4 and 5.
Please bear with us. This is not a commercial product and thus we cannot
spare the time for supporting it. BUT, if you should find a major bug do
let us know and hopefully we can correct it in a future release.
We encourage all users of the NNSYSID toolbox to write us about their
successes (and failures?). We are very interested in hearing where the
toolbox is used and for what type of applications. Since your comments
very well may influence future releases of the toolbox this is also in
your own interest! You can e-mail your experiences to any of the people
listed at the bottom of this page.
| AN
ADD-ON FOR CONTROL DESIGN |
If you are interested in neural networks for control we recommend that
you download our NNCTRL toolkit. See our
NNCTRL
toolkit page for supplementary information.
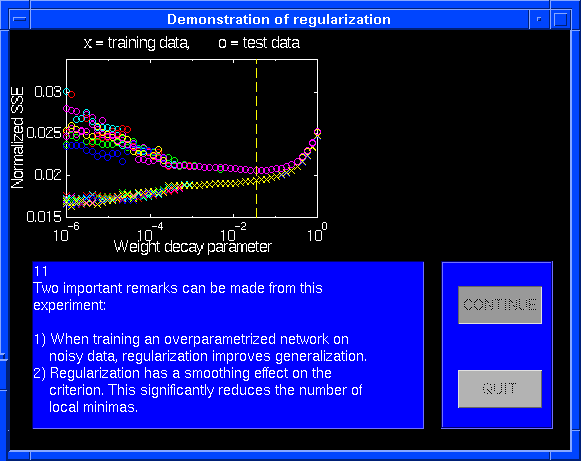
Images from "test6" which illustrate some of the effects of regularization
by simple weight decay. On a simple curve-fitting example it is shown how
weight decay improves generalization and that it moreover has a "smoothing"
effect on the criterion, which significantly reduces the number of local
minimas. 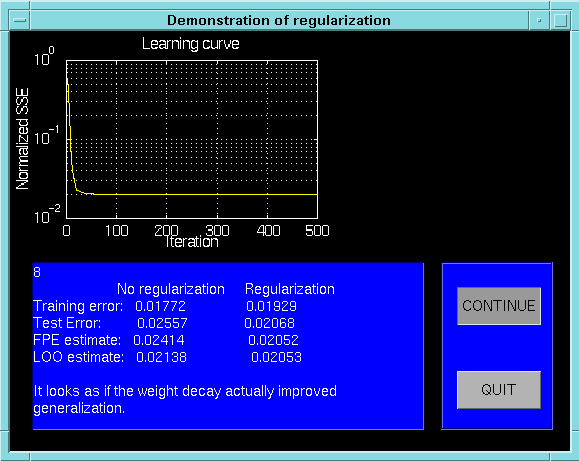
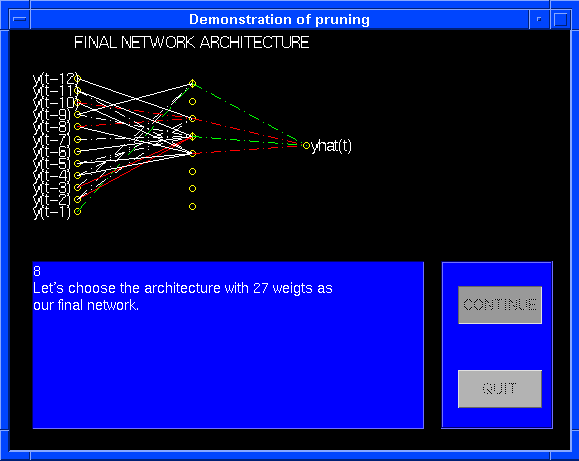
"test7" shows how pruning by "optimal brain surgeon" can be used for
determining the optimal network archtecture. The subject of investigation
is here the well-known sunspot benchmark timeseries. From an initial fully
connected network architecture with 113 weights, the network is pruned
until an architecture with only 27 weights appears.
The toolbox functions grouped by subject
|
FUNCTIONS FOR TRAINING
|
| batbp |
Batch version of the back-propagation algorithm |
| incbp |
Recursive (/incremental) version of back-propagation |
| igls |
Iterated Generalized Least Squares training of multi-output
nets |
| marq |
Levenberg-Marquardt method |
| marqlm |
Memory-saving implementation of the Levenberg-Marquardt
method |
| rpe |
Recursive prediction error method |
|
|
FUNCTIONS FOR PREPARATION OF
DATA
|
| dscale |
Scale data to zero mean and variance one |
|
|
FUNCTIONS FOR TRAINING MODELS
OF DYNAMIC SYSTEMS
|
| lipschit |
Determine the lag space |
| nnarmax1 |
Identify a Neural Network ARMAX (or ARMA) model (Linear
MA filter) |
| nnarmax2 |
Identify a Neural Network ARMAX (or ARMA) model |
| nnarx |
Identify a Neural Network ARX (or AR) model |
| nnarxm |
Identify a multi output Neural Network ARX (or AR) model. |
| nnigls |
Iterated Generalized LS training of multi-output NNARX models. |
| nniol |
Identify a Neural Network model suited for I-O linearization
control |
| nnoe |
Identify a Neural Network Output Error model |
| nnrarmx1 |
Recursive counterpart to NNARMAX1 |
| nnrarmx2 |
Recursive counterpart to NNARMAX2 |
| nnrarx |
Recursive counterpart to NNARX |
| nnssif |
Identify a NN State Space Innovations form model |
|
|
FUNCTIONS FOR PRUNING NETWORKS
|
| netstruc |
Extract weight matrices from matrix of parameter vectors |
| nnprune |
Prune models of dynamic systems with Optimal Brain Surgeon
(OBS) |
| obdprune |
Prune feed-forward networks with Optimal Brain Damage (OBD) |
| obsprune |
Prune feed-forward networks with Optimal Brain Surgeon (OBS) |
|
|
FUNCTIONS FOR EVALUATING TRAINED
NETWORKS
|
| fpe |
FPE estimate of the generalization error for feed-forward
nets |
| ifvalid |
Validation of models generated by NNSSIF |
| ioleval |
Validation of models generated by NNIOL |
| kpredict |
k-step ahead prediction of dynamic systems. |
| loo |
Leave-One-Out estimate of generalization error for feed-forward
nets |
| nneval |
Validation of feed-forward networks (trained by marq,rpe,bp) |
| nnfpe |
FPE for I/O models of dynamic systems |
| nnloo |
Leave-One-Out estimate for NNARX models. |
| nnsim |
Simulate model of dynamic system from sequence of inputs |
| nnvalid |
Validation of I/O models of dynamic systems |
| wrescale |
Rescale weights of trained network |
| xcorrel |
Calculates high-order cross-correlation functions |
|
|
MISCELLANOUS FUNCTIONS
|
| Contents |
Contents file |
| drawnet |
Draws a two layer neural network |
| getgrad |
Derivative of network outputs w.r.t. the weights |
| pmntanh |
Fast tanh function |
|
|
DEMOS
|
| test1 |
Demonstrates different training methods on a curve fitting
example |
| test2 |
Demonstrates the NNARX function |
| test3 |
Demonstrates the NNARMAX2 function |
| test4 |
Demonstrates the NNSSIF function |
| test5 |
Demonstrates the NNOE function |
| test6 |
Demonstrates the effect of regularization by weight decay |
| test7 |
Demonstrates pruning by OBS on the sunspot benchmark problem |
|
For more information, please contact one of the following:
Magnus Nørgaard,
Ole Ravn, or
Paul H. Sørensen,
|



