a) Al existir simetría cilíndrica, para el cálculo del campo eléctrico aplicamos el Teorema de Gauss a una superficie cilíndrica de radio r y longitud L y cuyo eje coincide con el eje del sistema:
Para r<R1:
Por la simetría del problema la superficie lateral del cilindro es una superficie equipotencial, por lo tanto el campo eléctrico será perpendicular a dicha superficie y por las bases del cilindro el flujo será nulo ya que en esos puntos el vector campo eléctrico y el vector superficie son perpendiculares. Así mismo el módulo del campo eléctrico sólo depende de r, y tiene el mismo valor en todos los puntos de la superficie lateral. De este modo, tenemos:
![]()
La carga en el interior de esta superficie a través de la cual estamos calculando el flujo es:
![]()
donde se ha tomado como diferencial de volumen una corteza cilíndrica de espesor dr. Así, nos queda para el campo eléctrico en el interior del conductor de radio R1, la expresión:
![]()
En el interior del dieléctrico, para R1 < r < R2, procediendo de forma análoga tenemos:
![]()
siendo la carga encerrada la total de la distribución volumétrica:
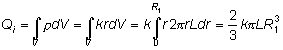
y quedando para el campo eléctrico la expresión:
![]()
Para puntos situados en el interior del conductor conectado a tierra (R2 < r < R3) el campo eléctrico es nulo.
Para r > R3, el campo eléctrico también es nulo, dado que el conductor externo es una pantalla eléctrica y separa desde el punto de vista electrostático el exterior de las cargas interiores.
Respecto a los potenciales, tenemos:
En el exterior, para r > R3, y en el conductor conectado a tierra R2<r<R3, el potencial es constante, por ser E=0, y su valor es cero, dado que el conductor se encuentra conectado a tierra.
En el dieléctrico, R1 < r < R2:
![]()
Para hallar la constante de integración, tenemos en cuenta el valor conocido del potencial en R2, V(R2)=0, ya que al ser la función potencial continua y uniforme su valor en R2 debe coincidir al calcularlo por la expresión anterior. Así, tenemos:
![]()
Para el potencial nos queda entonces:
![]()
En el interior de la distribución de carga (r<R1):
![]()
Para conocer la constante de integración procedemos como en el caso anterior, sabiendo que el potencial debe cumplir la condición de continuidad:
![]()
Quedando para el potencial en el interior:
![]()