b) Tomamos el camino que sigue el sentido de la intensidad:

De haber seguido el camino contrario al indicado por la intensidad, dado que existe un receptor en el mismo, tendríamos que haber calculado V_B -V_A y después haberle cambiado de signo:

Luego,

V_A - V_B = - (V_B - V_A) = 12,5 V

obteniendo por lo tanto el mismo valor.

c) Será la suma de las pérdidas por efecto Joule más las potencias transformadas en receptores y en el generador de 5V que consume potencia:

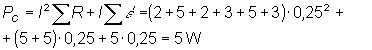
Podríamos haber calculado directamente la potencia total generada P=20·0,25 =5 W y dado que se tiene que cumplir que su valor es igual a la potencia total consumida, el apartado estaría resuelto.

d) Solo suministra potencia el generador de f.e.m. 20 V. Su potencia generada:

P_g = e I = 20·0,25 = 5 W

coincide con la potencia total consumida por el circuito, lo cual era de esperar dado que tiene que cumplirse el balance de potencias en el circuito:

Potencia total generada = Potencia total consumida

La potencia que suministra será la que resulta de restar las pérdidas internas:

P_S = P_g - P_J = 5 - 2·0,25² = 4,875 W

e) La intensidad que circula por el circuito en este caso sigue la expresión:

y la potencia consumida en un receptor:

P_C = 5I + 3I²

dicha potencia debe ser igual a 8W, de dónde,