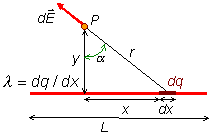
En este caso tomaremos la carga elemental dq situada en una longitud
elemental dx sobre la distribución. El campo que crea en el punto P es:La metodología para resolver este problema, aplicable también a muchos otros, consiste en dividir primero la distribución en cargas elementales, después aplicar las expresiones del campo o potencial electrostático creado por cargas puntuales y, finalmente, sumar (integrar) los valores de estas magnitudes para toda la distribución.
En este caso tomaremos la carga elemental dq situada en una longitud
elemental dx sobre la distribución. El campo que crea en el punto P es:
siendo 
el vector unitario en la dirección que une la carga elemental y el punto. En
función de la densidad lineal de carga l la carga elemental será dq = l dx, y la expresión anterior queda:
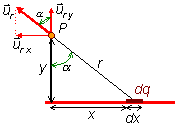Para calcular el campo total es necesario sumar (integrar) para toda la
distribución de carga la expresión anterior. Dicha integración es más sencilla si se
utiliza como variable de integración el ángulo a de la figura. Para ello debemos representar r, x y 
en función de dicho ángulo.
como y es constante,
Por otro lado,
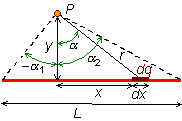De este modo, 
es
igual a,
Ahora debemos integrar dicha expresión. En la figura se representa una distribución de longitud L en la cual los límites de integración para la variable a vienen dados por -a1 y a2. De este modo, el campo eléctrico viene dado por:
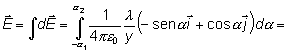
