 La existencia de una simetría respecto al plano XY, permite que este
problema pueda también ser resuelto mediante el teorema de Gauss. Dada la simetría del
problema, planos paralelos al plano cargado son superficies equipotenciales, por lo que el
módulo del campo eléctrico solo depende de la distancia z al plano XY, y
además, la dirección del campo eléctrico debe ser perpendicular a dichos planos, es
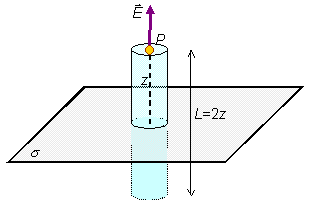
decir, dirección en el eje Z. Por tanto, podemos utilizar como superficie de Gauss
un cilindro de longitud L y radio R, situado perpendicularmente al plano, y
de tal modo que la distancia de las dos bases al plano es la misma, tal y como indica la
figura.
La existencia de una simetría respecto al plano XY, permite que este
problema pueda también ser resuelto mediante el teorema de Gauss. Dada la simetría del
problema, planos paralelos al plano cargado son superficies equipotenciales, por lo que el
módulo del campo eléctrico solo depende de la distancia z al plano XY, y
además, la dirección del campo eléctrico debe ser perpendicular a dichos planos, es
decir, dirección en el eje Z. Por tanto, podemos utilizar como superficie de Gauss
un cilindro de longitud L y radio R, situado perpendicularmente al plano, y
de tal modo que la distancia de las dos bases al plano es la misma, tal y como indica la
figura.
El flujo del campo eléctrico viene dado por,
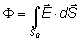
en esta integral, para la superficie lateral del
cilindro el vector 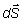 y el
campo eléctrico son perpendiculares, por lo que su producto escalar es nulo. De este
modo, a la integral del flujo solamente contribuyen la base superior (Bs) y la base
inferior (Bi) del cilindro:
y el
campo eléctrico son perpendiculares, por lo que su producto escalar es nulo. De este
modo, a la integral del flujo solamente contribuyen la base superior (Bs) y la base
inferior (Bi) del cilindro:
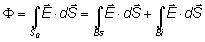
como además, en las bases del cilindro, el campo
eléctrico es paralelo al vecotr superficie, constante en toda la superficie, y con el
mismo módulo para las dos bases del cilindro, obtenemos,
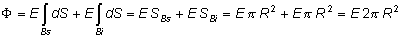
Aplicando ahora el teorema de Gauss,
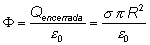
e igualando ambas expresiones,
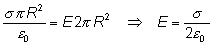
y, como habíamos comentado anteriormente, la dirección del campo
es en el eje Z, de modo que escrito vectorialmente queda:
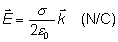
 La existencia de una simetría respecto al plano XY, permite que este
problema pueda también ser resuelto mediante el teorema de Gauss. Dada la simetría del
problema, planos paralelos al plano cargado son superficies equipotenciales, por lo que el
módulo del campo eléctrico solo depende de la distancia z al plano XY, y
además, la dirección del campo eléctrico debe ser perpendicular a dichos planos, es
decir, dirección en el eje Z. Por tanto, podemos utilizar como superficie de Gauss
un cilindro de longitud L y radio R, situado perpendicularmente al plano, y
de tal modo que la distancia de las dos bases al plano es la misma, tal y como indica la
figura.
La existencia de una simetría respecto al plano XY, permite que este
problema pueda también ser resuelto mediante el teorema de Gauss. Dada la simetría del
problema, planos paralelos al plano cargado son superficies equipotenciales, por lo que el
módulo del campo eléctrico solo depende de la distancia z al plano XY, y
además, la dirección del campo eléctrico debe ser perpendicular a dichos planos, es
decir, dirección en el eje Z. Por tanto, podemos utilizar como superficie de Gauss
un cilindro de longitud L y radio R, situado perpendicularmente al plano, y
de tal modo que la distancia de las dos bases al plano es la misma, tal y como indica la
figura.