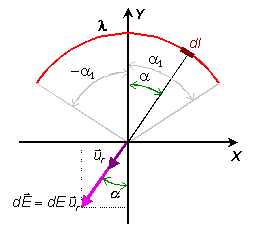
a) El campo elemental, ![]() , creado por el elemento de longitud dl en O (que
tiene una carga dq = l dl), es
igual a:
, creado por el elemento de longitud dl en O (que
tiene una carga dq = l dl), es
igual a:
![]()
Observa que en este caso la distancia r de la carga dq al punto O(0,0) donde se está calculando el campo es constante, y vale R.
Integrado ![]() a lo largo
de todo el arco, obtendremos el campo total:
a lo largo
de todo el arco, obtendremos el campo total: ![]()
![]()
 Para resolver la integral conviene hacer un cambio de variable, e integrar
respecto del ángulo a, en
lugar de integrar respeto de l. La relación entre el ángulo a y el arco l es,
Para resolver la integral conviene hacer un cambio de variable, e integrar
respecto del ángulo a, en
lugar de integrar respeto de l. La relación entre el ángulo a y el arco l es,
![]()
El vector unitario, ![]() , viene dado por (ver figura):
, viene dado por (ver figura):
![]()
En la variable angular a los límites de integración serán entre -a1 y a1:
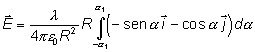
Calculando la integral de cada uno de los sumandos del integrando, obtenemos:
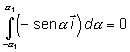
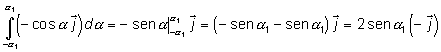
Con lo cual, el campo total es igual a,
![]()