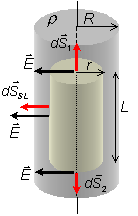
a) Al tratarse de un cilindro indefinido, nos permite resolver este problema mediante el teorema de Gauss. Dada la simetría del problema, el módulo del campo eléctrico solo depende de la distancia r al eje del cilindro, y además, la dirección del campo eléctrico debe ser radial. Por tanto, podemos utilizar como superficie de Gauss un cilindro de longitud L y radio r, coaxial al cilindro cargado.

r < R:

En este caso al ser r más pequeño que R, la superficie de Gauss está contenida dentro del cilindro, tal y como indica la figura.

El flujo del campo eléctrico a través de la superficie de Gauss es,

dicha integral la podemos dividir en tres partes, el flujo a través de la superficie lateral (SL), y el flujo a través de cada una de las bases del cilindro (B₁ y B₂),

Para las dos bases del cilindro, el vector es perpendicular a la superficie, tal y como indica la figura, mientras que el campo eléctrico tiene la dirección radial. Por tanto, son vectores perpendiculares, y su producto escalar es cero. Por otro lado, para la superficie lateral del cilindro, el vector es radial, paralelo al campo eléctrico:

El campo eléctrico solamente depende de la distancia al eje del cilindro, por tanto en la superficie lateral del mismo es constante, y puede salir fuera de la integral,

la integral de dS es la superficie lateral del cilindro, que es igual a 2prL.

Por otro lado, el teorema de Gauss nos dice que el flujo es igual a la carga encerrada en el interior de la superficie dividido por ,

y la carga encerrada en el interior es igual a la densidad de carga por el volumen,

Igualando ambas expresiones del flujo obtenemos el valor del campo eléctrico,

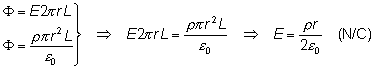
Que como se ve, es directamente proporcional a r, es decir, es creciente con el radio.

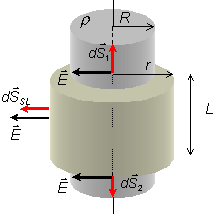
r > R:

De nuevo, tomamos como superficie de Gauss un cilindro de radio r y longitud L. En este caso al ser r más grande que R, la superficie de Gauss se sitúa fuera del cilindro cargado, tal y como indica la figura.

Siguiendo el mismo razonamiento que en el caso anterior, el flujo a través de la superficie de Gauss será,

Aplicando ahora el teorema de Gauss,

donde en este caso, la carga encerrada es aquella contenida en un cilindro de longitud L, y radio R,

Observa que la diferencia con el caso anterior radica en que ahora aparece R en lugar de r en esta expresión.

Igualando las dos expresiones del flujo obtenidas, podemos calcular el módulo del campo eléctrico:

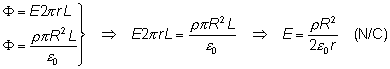
que en este caso es inversamente proporcional a la distancia r.

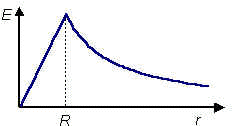Si representamos el módulo del campo eléctrico en función de la distancia r, obtenemos la función indicada en la figura, donde se ve que para r < R el campo crece linealmente con r, y para r > R, el campo decrece de forma inversamente proporcional r.