crea en el punto P un diferencial de campo:Un elemento de corriente crea en el punto P un diferencial de campo:
Vemos en la figura que 
son perpendiculares para cualquier punto de la espira circular,
luego el módulo de 
, nos
queda:
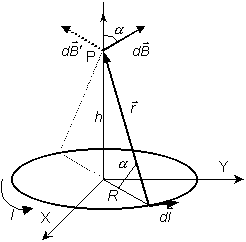y su dirección es normal al plano
determinado por .
La resolución de la integral vectorialmente plantea dificultades, pues
varían de dirección.
Podemos simplificar el problema considerando las simetrías del mismo. 
La componente de sobre la normal al eje se anula con la componente, también sobre la
normal al eje, del vector
creado por un elemento de corriente 
simétrico del 
Así, el campo en el punto P del eje de la espira circular tiene la
dirección del propio eje y su módulo es:
y sustituyendo en la anterior expresión la relación: 
, resulta:
ésta expresión la podemos escribir en función de la distancia h del punto P al centro de la espira, r2 = h2 + R2 y nos queda:
También podemos expresar el mismo resultado en función del momento magnético de la espira (m = i
pR2), ya que su dirección y sentido coinciden con los del campo magnético. Así, tenemos: