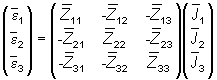
En este problema tenemos una red de corriente alterna. El método de resolución es el mismo que se aplicaría a un circuito de corriente continua, solo que las magnitudes que aparecen en este caso vienen representadas por números complejos, en lugar de números reales.
a) Para aplicar el método de las mallas, en primer lugar, y puesto que todos los generadores que aparecen son generadores de tensión, numeraremos las mallas y fijamos un sentido único para las intensidades de malla, tal y como indica la figura.
De este modo, la ecuación matricial que se obtiene por aplicación del método de las mallas es:
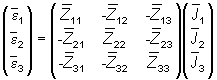
donde ![]() es el sumatorio de las fuerzas electromotrices de la malla i,
es el sumatorio de las fuerzas electromotrices de la malla i, ![]() , es la suma de las impedancias
de la malla i, y
, es la suma de las impedancias
de la malla i, y ![]() son las impedancias comunes a la malla i y a la malla j. Sustituyendo los
valores correspondientes se obtiene:
son las impedancias comunes a la malla i y a la malla j. Sustituyendo los
valores correspondientes se obtiene:
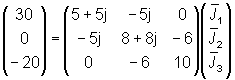
Observa que la fuerza electromotriz de la malla 3, ![]() , es negativa, puesto que la
intensidad
, es negativa, puesto que la
intensidad ![]() entra por el
borne positivo del generador.
entra por el
borne positivo del generador.
La intensidad ![]() pedida
coincide con la intensidad de malla
pedida
coincide con la intensidad de malla ![]() , con lo cual bastará calcular dicha intensidad para resolver el
problema:
, con lo cual bastará calcular dicha intensidad para resolver el
problema:

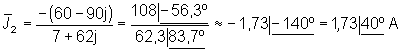
b) Para aplicar ahora el método de los nudos, un primer paso a realizar es la transformación de las fuentes de tensión a fuentes de intensidad. Así obtenemos que:
![]()
![]()
Con la polaridad indicada en la figura.
![]()
![]()
Con la polaridad indicada en la figura.
Con lo cual, sustituyendo también las impedancias por sus correspondientes admitancias, el circuito queda:
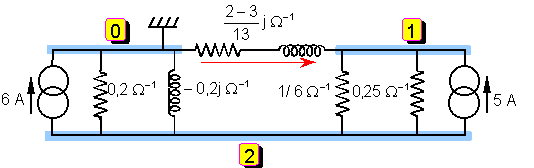
En el circuito tenemos 3 nudos, indicados en la figura. A la hora de
numerarlos tenemos en cuenta que la variable que queremos conocer, ![]() , nos exige hallar únicamente la diferencia de
potencial en los bornes de la admitancia por la que circula. Por ello tomaremos como nudo
de referencia uno de los bornes de dicha admitancia, limitando de esta forma nuestro
problema a hallar el valor de una única variable (
, nos exige hallar únicamente la diferencia de
potencial en los bornes de la admitancia por la que circula. Por ello tomaremos como nudo
de referencia uno de los bornes de dicha admitancia, limitando de esta forma nuestro
problema a hallar el valor de una única variable (![]() , según la numeración indicada en la figura).
, según la numeración indicada en la figura).
El resultado final del ejercicio no depende del nudo de referencia que se tome. Dicho nudo de referencia no tiene por que coincidir con el nudo que originalmente estaba conectado a tierra.
La ecuación matricial del método de los nudos es,
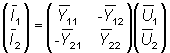
donde ![]() representa la
intensidad que entra en el nudo i,
representa la
intensidad que entra en el nudo i, ![]() , es la suma de las admitancias que concurren en el nudo i, e
, es la suma de las admitancias que concurren en el nudo i, e ![]() son las admitancias comunes al
nudo i y al nudo j. Sustituyendo los valores correspondientes se obtiene:
son las admitancias comunes al
nudo i y al nudo j. Sustituyendo los valores correspondientes se obtiene:
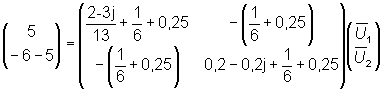
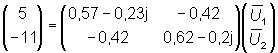
Observa que las intensidades en el nudo 2 aparecen con signo negativo, puesto que son intensidades que salen de dicho nudo.
De la expresión anterior obtenemos el potencial para el nudo 1:
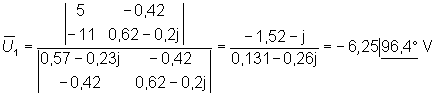
Y con ello calculamos finalmente la intensidad ![]() :
:
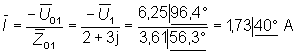
c) El valor instantáneo de la intensidad viene dado por la expresión: i(t) = Im cos(
wt + j i ) donde![]()
y la pulsación y la diferencia de fase son:
w
= 2pf = 2 p 100 = 628,32 rad/sj i = 40º
Luego la intensidad instantánea viene dada por
i(t) = 2,45 cos(628,32 t + 40º) A