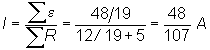a) Para resolver este ejercicio de forma más sencilla, conviene sustituir las dos resistencias de 6 W situadas en paralelo, por su resistencia equivalente:
y una vez hecho este paso previo, podemos resolver el problema por el método de las mallas.
Para aplicar el método de
las mallas, primeramente habría que transformar todos los generadores de intensidad del
circuito en generadores de tensión. En este caso, puesto que no hay ningún generador de
intensidad, este paso no es necesario realizarlo.
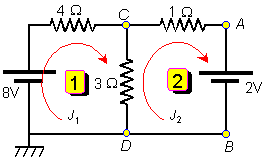
En segundo lugar hay que numerar las mallas, y asignar a cada una de ellas una intensidad de malla, todas en el mismo sentido. En este caso hay dos mallas, que numeramos de izquierda a derecha, y les asignamos las intensidades de malla en sentido de las agujas del reloj, tal y como indica la figura.
La ecuación matricial que se obtiene por aplicación del método de las mallas es,
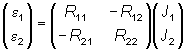
donde
ei representa la suma de las fuerzas electromotrices de la malla i, Rii es la suma de las resistencias de la malla i, y Rij es la suma de las resistencias comunes a la malla i y a la j. Sustituyendo ahora los valores se obtiene,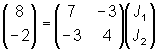
Observa que la fuerza electromotriz de la malla 2, e2, es negativa debido a que la intensidad J2 atraviesa el generador del borne positivo al negativo del mismo.
La intensidad que circula de A a B (IAB) es igual a J2, que aplicando la regla de Cramer viene dada por:
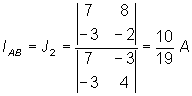
La intensidad J1 viene dada por,
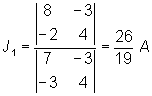
b) Para
determinar el equivalente de Thevenin necesitamos la resistencia equivalente de la red
pasiva, y la diferencia de potencial, entre los puntos C y D.
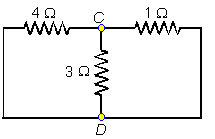
Observando la figura vemos que las tres resistencias del circuito están conectadas en paralelo, de modo que la resistencia equivalente entre los puntos C y D viene dada por:
La diferencia de potencial entre C y D viene dada por:
donde la intensidad ICD es igual a la intensidad de la malla 1 menos la intensidad de la malla 2:
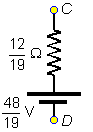
con lo cual
De este modo, el equivalente de Thevenin entre los puntos C y D es el indicado en la figura, con el borne negativo en el punto D
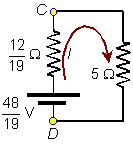c) Si
colocamos ahora una resistencia de 5 W entre los puntos C
y D, y utilizando el equivalente de Thevenin tal y como indica la figura, la
intensidad viene dada por:
