n×m=p
Û
![]()
CONCEPTOS BÁSICOS
· Historia sobre los conjuntos de los números
· El conjunto de los números naturales N
· El conjunto de los números enteros Z
· El conjunto de los números racionales Q
· El conjunto de los números reales R
· El conjunto de los números complejos C
· Identidades de uso frecuente
· Historia sobre el conjunto de los números
El conjunto de los números naturales N
El conjunto de los Números Naturales N, tiene una definición axiomática, que viene dada
por los Axiomas
de Peano.
· Operaciones o leyes definidas en N
En N
pueden definirse la Suma entre números
naturales, que resulta ser una ley interna (por operar con números de un
conjunto y obtener como resultado otro número perteneciente al mismo conjunto),
mediante:
n+m=p Û
p es el resultado de aplicar el siguiente n veces a m
Y también se define la operación Producto,
tal que:
n×m=p
Û
![]()
Esto
conduce a definir una nueva operación, denominada Resta,
como sigue:
p-n=m Û n+m=p
Pero
aquí empiezan a surgir determinadas cuestiones que conllevan la necesidad de
ampliar el conjunto de los números conocidos hasta el momento. Tales “problemas”
o pegas son las siguientes:
a). ¿Qué ocurrirá si en la nueva operación definida, la resta p = n ?.
Todos, a día de hoy, sabemos que el resultado será el número 0 pero éste no existía como natural en ese momento; y aún hay más…
b). ¿Y si en la misma operación
resta, ocurre que n >p?.
También
a día de hoy sabemos que la respuesta a esta pregunta son los Números Enteros,
o el conjunto conocido como Z.
Surge así la necesidad de ampliar el conjunto de números que existía hasta el
momento, con el nuevo conjunto de los Números Enteros y que, como ya hemos
indicado, se denotará por Z,
del cual daremos la definición en la siguiente sección.
Vendrá
dado por la aplicación que sirve para construir dichos números, la aplicación
siguiente, que una vez introducida la
operación resta podemos entenderlo
como sigue:
n<m
Û m-n ³1
ó
también puede definirse dicha relación de orden como:
n<m Û $ pÎ N tal que m+p=n
Verdaderamente, para que una relación sea de orden, debe verificar una serie de propiedades que aquí no vamos a detallar. Al orden que hemos definido en N se le llama orden natural.
· Principio del primer elemento
Para todo subconjunto no vacío de los naturales A Í N existe un elemento mínimo o primer elemento; es decir, es igual a sí mismo y menor que todos los demás. Evidentemente, este primer elemento es el número natural 1.
El
conjunto de los números enteros Z
Indicar, en primer lugar, que denotaremos con –A al conjunto cuyos elementos
sean los de A con el signo opuesto, es decir:
bÎ-A
Û $
a ÎA
tal que b = -a
Z: =NÈ{0}È(- N): ={…,-3,-2,-1,0,1,2,3,…}
·
Operaciones definidas en Z
Las operaciones definidas en Z son las mismas que en N , pero ahora los problemas de los que hablábamos antes (link a esos problemas), ya no suceden al introducir el 0 y los números negativos. Habrá que extender, sin embargo, los conceptos anteriores, para los números negativos.
·
Suma
Consideremos a,b Î N, y por tanto con –a y –b Î- N. Así indicaremos ahora sólo los casos no contemplados en la operación suma definida en N:
(-a)+(-b)=-a-b=-(a+b)
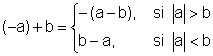
·
Producto.
Regla de los signos
+
×+ = +
+
× - = -
-
× + = +
- × - = -
·
Orden
en Z
Ahora ya podemos definir la relación de orden
entre números enteros. Esta relación ya no es un orden natural como ocurría
en N,
sino que es una ordenación natural
inducida que se define como sigue:
Dados
p, q Î Z , p
![]() q Û q-p=0 ó
q-p Î N
q Û q-p=0 ó
q-p Î N
m
× x = p
no es resoluble en Z, y esto crea la necesidad de introducir un nuevo conjunto, donde podamos resolver dicha ecuación, es decir, donde el resultado de ese producto dé un número del conjunto creado. Surge así el conjunto de los Números Racionales, que denotaremos como Q.
El conjunto de los números racionales Q
Estos
se introdujeron al intentar resolver la ecuación ax=b, (siendo a no nulo y a,b enteros) surge,
de forma natural la fracción
![]() .
.
Se define la relación de equivalencia
![]()
si
y sólo si
![]() , llamando clase de equivalencia al conjunto de fracciones que representan lo
mismo. Cada clase de equivalencia se llama número racional. De cada clase de
equivalencia elegiremos la fracción más idónea para trabaja con ella y que
llamaremos fracción canónica:
, llamando clase de equivalencia al conjunto de fracciones que representan lo
mismo. Cada clase de equivalencia se llama número racional. De cada clase de
equivalencia elegiremos la fracción más idónea para trabaja con ella y que
llamaremos fracción canónica:
![]()
tal
que a Î
N
y b Î
Z
(donde
a y b son primos entre sí).
El conjunto de los números racionales se representa por Q . Entonces:
![]()
·
Estructura
algebraica de Q
Se definen en Q las siguientes operaciones:
¨ Suma:
![]()
¨Producto:
![]()
Vamos
a representar en adelante los números racionales por letras del alfabeto: a, b,
c …
Con
la operación suma, Q
tiene las siguientes propiedades:
| Asociativa | (a+b)+c = a+(b+c) " a,b,c Î Q |
| Elemento neutro | $ e Î Q / " a Î Q Þ a + e = e + a = a |
| Elementos simétricos (opuestos) | " aÎQ, $ (-a)ÎQ / a +(-a) =(-a) + a = 0 |
| Conmutativa | a+b = b+a " a,b Î Q |
Se dice, con esto que (Q,+)
es un GRUPO
CONMUTATIVO.
Con la operación producto, Q tiene las siguientes propiedades:
| Asociativa | (a· |
| Elemento neutro | $
e Î
Q
/ "
a Î
Q
Þ
a · |
| Elementos simétricos (opuestos) | " aÎQ*, $ (1/a)ÎQ* / a·(1/a)=(1/a)·a =1 |
| Conmutativa | a
· |
Se
dice, con esto que (Q,+)
es un GRUPO
CONMUTATIVO.
Además, en Q
también se verifica la propiedad:
|
Distributiva |
|
Con
estas nueve propiedades, se dice que (Q,+)
es un CUERPO
CONMUTATIVO.
El conjunto de los números reales R
Al
plantear el problema de calcular la longitud de la hipotenusa de un triángulo
rectángulo cuyos catetos midan una unidad, tenemos, al aplicar el teorema de
Pitágoras: h2
= 2
.
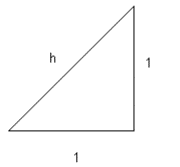 Esta
ecuación no se puede resolver en Q,
porque si existiera un número racional
Esta
ecuación no se puede resolver en Q,
porque si existiera un número racional
![]() que fuera una fracción canónica,
tendríamos que:
que fuera una fracción canónica,
tendríamos que:
![]()
el 2 divide a b2
y por tanto, también a b, luego b=2k
.
Así
pues: (2k)2 = 2a2 Û2k2
= a2
luego 2 divide a b y como consecuencia
![]() no es canónica puesto que se puede
simplificar por 2.
no es canónica puesto que se puede
simplificar por 2.
Esto significa que los números racionales son insuficientes para medir la
longitud de ciertos segmentos, lo cuál significa que deben existir otros números,
que llamaremos irracionales, que serán los números x que verifican la ecuación
x2
= a,
(a positivo) y que representaremos por
![]() .
.
Definiremos el conjunto de los números irracionales como el conjunto de todos
los números decimales de infinitas cifras no periódicas. Se representa por I.
La unión del conjunto de los números racionales con el de los irracionales constituye el conjunto de los números reales. Se representa por R.
![]()
(R,+,·)
es un CUERPO
CONMUTATIVO.
El conjunto de los números complejos C
En
el cuerpo de los números reales se pueden realizar siempre las cuatro
operaciones fundamentales: sumar, restar, multiplicar y dividir (salvo por cero)
y además la raíz cuadrada de los números positivos, pero todavía hay
operaciones como la raíz cuadrada de un número negativo que no tienen solución
en R.
Se introduce, pues un nuevo conjunto de números, que llamaremos complejos donde se puedan resolver todas las ecuaciones que se resolvían en el cuerpo de los reales, (por tanto debe contener a R) y además las del tipo
![]()
Por ejemplo, para resolver x2 + 1 = 0, introducimos la unidad imaginaria o j:
![]()
Al conjunto de los números complejos se le representa por C y se define:
![]()
Se definen en C las siguientes operaciones:
¨Suma:
![]()
¨Producto:
![]()
(c,+)
es un GRUPO
CONMUTATIVO y (c,+,·)
es un CUERPO
CONMUTATIVO.
![]()
· Identidades de uso frecuente
|
(a+b)2 = a2 + 2ab + b2 |
| (a-b)2 = a2 - 2ab + b2 |
| (a+b)3 = a3 + 3a2b + 3ab2 + b3 |
| (a-b)3 = a3 - 3a2b + 3ab2 - b3 |
| (a+b)(a-b) = a2 - b2 |
| (a+b+c)2 = a2 + b2 + c2 +2ab +2ac +2bc |
· Como aplicación de la regla de Ruffini
![]()
Nota: si m es impar, la división es exacta
Ejemplo:
![]()
Ejemplo:
![]()
![]()
Ejemplo:
![]()
Ejemplo:
![]()
![]()
Nota:
si m es par, la división es exacta
Ejemplo:
![]()
Ejemplo:
![]()
![]()
Ejemplo:
![]()
Ejemplo:
![]()
· Número Factorial
n! = n · (n-1) · ... · 2 ·
1 y por convenio
![]()
Ejemplo:
![]()
· Número Combinatorio
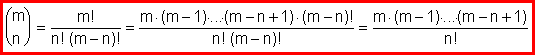
m
>n
·
Propiedades de
los números combinatorios
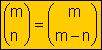
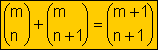
Ejemplo:
![]()
Ejemplo de aplicación posterior:
¿Cuántas parejas se
pueden formar con 5 personas?
![]()
Se llama Triángulo de Tartaglia, triángulo aritmético o de Pascal a una tabla que contiene en cada fila los números combinatorios del mismo numerador.
Esta tabla tiene forma de triángulo, los términos de los dos lados oblicuos valen siempre 1 y los demás términos son tales que cada uno es la suma de los dos que tiene debajo.
Es, en general, un procedimiento sencillo para calcular los números combinatorios.
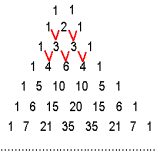
Con el nombre de binomio de Newton o fórmula del binomio entendemos el desarrollo de una potencia de un binomio, a+b en forma de polinomio ordenado.
![]()
![]()
![]()
Obsevando los coeficientes, se ve que coinciden con las primeras filas del triángulo de Tartaglia.
En general:
![]()
Ejemplo:
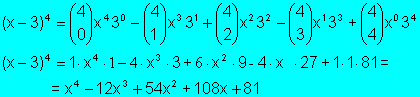
Nota: recordemos que a0 = 1 .