LÍMITES DE FUNCIONES Y CONTINUIDAD
· Límite de una función en un punto
· Límite de una suma de
funciones
· Límite
de un producto de funciones
· Límite
de un cociente de funciones
· Límite
de una potencia y una raíz
· Límite
de una función racional
· Límite
de expresiones irracionales
· Iniciación
al cálculo de límites
· Algunos
teoremas relacionados con funciones continuas
| Temas
relacionados:
|
· Límite de una función en un punto
Si f es una función definida en un intervalo real [a,b], y x0 es un punto de dicho intervalo, diremos que f(x) tiende a y0 cuando x tiende a x0 si a todo intervalo abierto que contenga a y0 , (es decir, un intervalo de la forma ] y0 - e , y0 + e [ cualquiera que sea e ), le corresponde un intervalo abierto que contiene a x0 (es decir, un intervalo de la forma ] x0 - d , x0 + d [ cualquiera que sea d ), y tal que si x ¹x0, xÎ[a,b] Ç ] x0 - d , x0 + d [ , entonces f( x)Î ] y0 - e, y0 + e [ .
Si esto se cumple, se dice que y0 es el límite de f(x) cuando x tiende a x0 y se escribe:
![]()
Esto equivale a decir que, a todo e > 0 , corresponde un d > 0 tal que
![]()
En los extremos del intervalo [a,b], podemos decir que
·
![]() ,
si a todo e
>
0
, corresponde un
d
> 0
tal que " x ¹
a, a < x < a+d
es ½f(x)-y0½<
e;
en este caso se dice que la función f(x) tiende a y0
cuando x tiende hacia a por la derecha y se escribe
,
si a todo e
>
0
, corresponde un
d
> 0
tal que " x ¹
a, a < x < a+d
es ½f(x)-y0½<
e;
en este caso se dice que la función f(x) tiende a y0
cuando x tiende hacia a por la derecha y se escribe
![]()
·![]() ,
si a todo e
>
0
, corresponde un
d
> 0
tal que " x ¹
b, b-d
< x < b
es ½f(x)-y0½<
e;
en este caso se dice que la función f(x) tiende a y0
cuando x tiende hacia b por la izquierda y se escribe
,
si a todo e
>
0
, corresponde un
d
> 0
tal que " x ¹
b, b-d
< x < b
es ½f(x)-y0½<
e;
en este caso se dice que la función f(x) tiende a y0
cuando x tiende hacia b por la izquierda y se escribe
![]()
En general, aun siendo x0 un punto interior del intervalo [a,b], denotaremos el límite por la derecha con la siguiente notación:
![]()
y el límite por la izquierda:
![]()
Una función puede tener en un punto x0 límite por la derecha y no por la izquierda (y viceversa), puede carecer de los dos, pueden existir los dos y ser iguales, o distintos, pero lo que no debemos olvidar es lo siguiente:
Si una función tiene límite en un punto, se cumple:
![]()
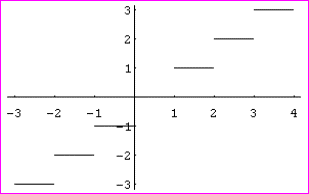
Ejemplo:
Recordemos la función E[x], (parte entera de x)
![]()
![]()
![]()
![]()
Supongamos que exista el![]() , puede suceder que tenga
, puede suceder que tenga
· el mismo valor que la imagen del punto x0 por la función f, (f(x0))
Aunque también puede ocurrir que no exista f(x0)
·
Propiedades
de los límites:
Si ![]() la función
f está acotada en un cierto entorno reducido
de
x0.
la función
f está acotada en un cierto entorno reducido
de
x0.
![]() >0, la función
f es
positiva en un
cierto entorno reducido
de
x0.
>0, la función
f es
positiva en un
cierto entorno reducido
de
x0.
Si
![]() <0, la función
f es
negativa en un
cierto entorno reducido
de
x0.
<0, la función
f es
negativa en un
cierto entorno reducido
de
x0.
Si ![]() ,
,
![]() ,
y
L<H, entonces f(x)<g(x) en un
cierto entorno reducido
de
x0.
,
y
L<H, entonces f(x)<g(x) en un
cierto entorno reducido
de
x0.
Si ![]() ,
,
![]() ,
y
en un
cierto entorno reducido
de
x0
se verifica que f(x)<g(x),
entonces L £
H.
,
y
en un
cierto entorno reducido
de
x0
se verifica que f(x)<g(x),
entonces L £
H.
El límite de una función en un punto, si existe, es único.
Si ![]() ,
,
![]() , y
f(x)<s(x)<g(x) en un
cierto entorno reducido
de
x0,
entonces
, y
f(x)<s(x)<g(x) en un
cierto entorno reducido
de
x0,
entonces ![]() .
.
Se dice que el límite de una función f(x) cuando x tiende hacia infinito es L si: " e>0, $ e>0 / ½x½>K Þ½f(x)-L ½<e. Se representa por:
![]()
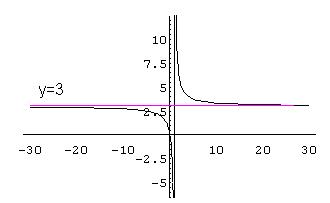
Ejemplo:
![]() .
Diremos que f(x) tiene una asíntota horizontal en la recta y=3 ya que
.
Diremos que f(x) tiene una asíntota horizontal en la recta y=3 ya que
![]()
·
Límite en más infinito
Se dice que el límite de una función f(x) cuando x tiende hacia más infinito es L si: " e>0, $ KÎR / x>K Þ½f(x)-L ½<e. Se representa por:
![]()
·
Límite en menos infinito
Se dice que el límite de una función f(x) cuando x tiende hacia menos infinito es L si: " e>0, $ KÎR / x<K Þ½f(x)-L ½<e. Se representa por:
![]()
Ejemplo:
Sea la función f(x) = 5x,
![]()
Se dice que el límite de una función f(x) es infinito cuando x tiende hacia x0 cuando: " MÎR, $ d>0 /0<½x-x0½<dÞ½f(x)½>M. Escribiremos:
![]()
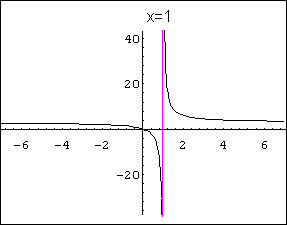
Ejemplo:
Sea la función![]() . Diremos que f(x) tiene una asíntota vertical en la recta x=1 ya que
. Diremos que f(x) tiene una asíntota vertical en la recta x=1 ya que
![]()
Análogamente
se definen los límites +¥,-¥:
¨ Se dice que el límite de una función f(x) es más infinito cuando x tiende hacia x0 cuando: " MÎ R, $ d>0 /0<½x-x0 ½<d Þ f(x) >M. Escribiremos:
![]()
¨ Se dice que el límite de una función f(x) es menos infinito cuando x tiende hacia x0 cuando: " MÎR, $ d>0 /0<½x-x0 ½<d Þ f(x) <M. Escribiremos:
![]()
· Infinitésimo
Diremos que f(x) es un infinitésimo en el punto x0 si tiene por límite 0 en x=x0.
![]()
·
Límite
de una suma de funciones
·
Sean dos funciones f y g,
a: finito o infinito
![]()
![]()
![]()
· Sean dos funciones f y g, a: finito o infinito
![]()
![]()
![]()
· Sean dos funciones f y g, a: finito o infinito
![]()
![]()
![]()
· Sean dos funciones f y g, a: finito o infinito
![]()
![]()
![]()
· Sean dos funciones f y g, a: finito o infinito
![]()
![]()
![]()
·
Límite
de un producto de funciones
·
Sean dos funciones f y g,
a: finito o infinito
![]()
![]()
![]()
· Sean dos funciones f y g, a: finito o infinito
![]()
![]()
![]()
· Sean dos funciones f y g, a: finito o infinito
![]()
![]()
![]()
· Límite de un cociente de funciones
· Sean dos funciones f y g, a: finito o infinito
![]()
![]()
![]()
· Sean dos funciones f y g, a: finito o infinito
![]()
![]()
![]()
· Sean dos funciones f y g, a: finito o infinito
![]()
![]()
![]()
· Sean dos funciones f y g, a: finito o infinito
![]()
![]()
![]()
· Límite de una potencia y de una raíz
·
Si
![]()
![]() y
y
![]() está definida en un
entorno de x0, entonces:
está definida en un
entorno de x0, entonces:
![]()
Cuando x tiende a ± ¥ el límite del polinomio es infinito con el mismo signo que su término de grado superior.
![]()
Ejemplo:
![]() .
.
·
Límite
de una función racional
Cuando x tiende a ± ¥ el límite de una función racional (cociente de polinomios) es el mismo que el del cociente de los términos de mayor grado de su numerador y su denominador.

Nota:
si para un cierto punto a se anulan
tanto numerador como denominador en una fracción, diremos que se presenta la
forma indeterminada![]() ,en
este caso, el límite de la fracción para x = a es el mismo que el de la
fracción que resulta de simplificar por x-a.
,en
este caso, el límite de la fracción para x = a es el mismo que el de la
fracción que resulta de simplificar por x-a.
Ejemplo:
![]()
·
Límite
de expresiones irracionales
Si en una fracción, la expresión
irracional se halla en el denominador (numerador), bastará con multiplicar
numerador y denominador por la expresión conjugada del denominador (numerador).
Ejemplo:

·
Iniciación al
cálculo de límites
Reglas básicas: a Î R - {0}

Indeterminaciones
![]()
·
Indeterminación
![]() (cociente
de polinomios):
(cociente
de polinomios):
El proceso a efectuar será dividir numerador y denominador por la x de
mayor potencia.
a).Grado del numerador
mayor:
Ejemplo:
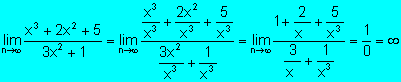
b).Grado del numerador y
denominador iguales:
Ejemplo:

c).Grado del denominador mayor:
Ejemplo:
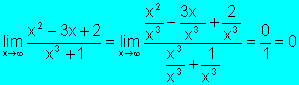
![]()
Ejemplo:
![]()
Ejemplo:
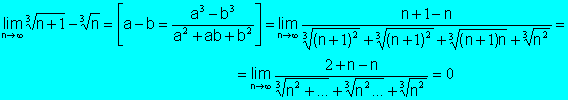
![]()
Ejemplo:

Recordar que:
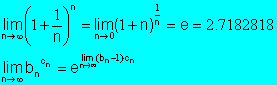
![]()
Ejemplo:
![]()
Una función definida en un intervalo real [a,b] se dice que es continua en un punto x0 si:
·
La función está definida en
·
![]()
Diremos que la función es continua en un intervalo
[a,b] si lo es en todos sus
puntos, lo cual implica que ha de estar definida en todos sus puntos, que en
todos sus puntos interiores debe tener límite por
la derecha, por la izquierda y que éstos han de ser iguales y tomar el
mismo valor que la función en dicho punto, además, en los extremos del
intervalo se debe cumplir: f(a+
) = f(a) y f(b-
) = f(b).
Ejemplo:
En el ejemplo anterior, la función E[x], (parte entera de x) es continua en los puntos interiores de cada subintervalo, pero no en los extremos, así podemos decir que es continua en los reales salvo los enteros.
·
Propiedades
de las funciones continuas:
Sean f(x), g(x) dos funciones continuas en [a,b] , entonces:
·
La
función (f+g)(x) es continua en [a,b]
·
La
función (fÑ
·
Si
la función ![]() es
continua en [a,b]
es
continua en [a,b]
·
La
función
·
Si
h(x) es una función continua en f([a,b]
Se deduce de todo ello:
Si
varias funciones son continuas en un mismo intervalo, toda función que resulte
de combinar las dadas mediante un número finito de operaciones es también
continua en el mismo intervalo, salvo en los puntos en los que no esté
definida.
Así pues son continuas las
siguientes funciones:
1.
La función
constante es continua en el cuerpo de los reales.
2.
La función
identidad es continua en el cuerpo de los reales.
3.
La función ![]() es continua en el cuerpo de los reales.
es continua en el cuerpo de los reales.
4.
La función polinómica
es continua en el cuerpo de los reales.
5.
La función racional
o cociente de polinomios es continua en el cuerpo de los reales, salvo en
aquellos valores que anulen el denominador.
Diremos
que una función es discontinua en un punto cuando no es continua en dicho
punto. Si representamos gráficamente una función discontinua, observaremos que
en dicho punto presenta un salto.
·
Tipos
de discontinuidades:
1). Evitable: cuando existe y es finito el
![]() , pero no existe el valor de la función en dicho punto f(x0). Se soluciona atribuyendo a la
función en el punto x0
el valor del límite.
, pero no existe el valor de la función en dicho punto f(x0). Se soluciona atribuyendo a la
función en el punto x0
el valor del límite.
Ejemplo:
Sea
![]() . En el punto x = 0 no está definida, pero sí el límite
. En el punto x = 0 no está definida, pero sí el límite
![]()

2). Inevitable: cuando existen tanto el
![]() como el valor de la función
en x0
, pero son distintos.
como el valor de la función
en x0
, pero son distintos.
Ejemplo:
Sea
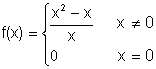
![]()
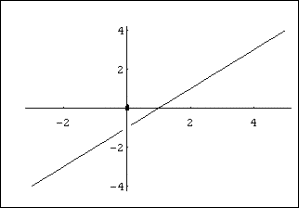
3). Inevitable: cuando existen (siendo finitos o infinitos) los límites
laterales pero son distintos.
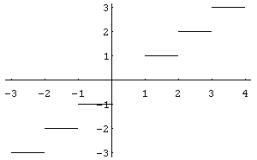
Ejemplo:
Observemos la siguiente gráfica en el punto x =2 (por ejemplo).
·
Algunos
teoremas relacionados con funciones continuas
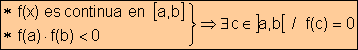
Se aplica en los procedimientos de cálculo aproximado de raíces de una ecuación, algebraica o trascendente relativamente complicada, en la que por lo general no resulta posible encontrar la solución exacta.
Supongamos que se tiene la ecuación
f(x) =0 (1)
donde
la función f(x) está definida y es continua en un intervalo finito o infinito
a<x<b.
Entenderemos por raíz
o cero de la ecuación (1) cualquier
valor a para el cual: f(a
)=0. Supondremos que esta ecuación tiene únicamente raíces separadas, es
decir, para cada raíz de la ecuación, existe un intervalo que no contiene a ninguna otra raíz .
Para la separación de raíces aplicaremos el
Teorema de Bolzano y la raíz a
será única si la función f(x) es
monótona , es decir, mantiene el signo en ]a,b[
. Conviene recordar que "Una ecuación algebraica de grado n posee a lo
sumo n raíces reales incluida su multiplicidad". Por consiguiente, si para
una ecuación de este tipo se obtienen n+1 cambios de signo, habrán quedado
separadas todas las raíces de la ecuación.
Si existe más de una raíz en el intervalo [a,b], la garantía del aislamiento podemos ofrecerla si se dan las condiciones del siguiente teorema
Teorema:
Si
f: ]a,b[ ®
R
es derivable en ]a,b[, f'(x)
¹
0, "x
Î ]a,b[, entonces, f es estrictamente monótona
(creciente o decreciente). O sea, su gráfica es siempre ascendente o siempre
descendente.
Teorema de Rolle-Bolzano:
Si f:[a,b] ®
R
continua, derivable en ]a,b[, f(a)f(b) < 0 y
f'(x) ¹
0,
Ejemplo:
Separa las raíces de la ecuación: x3
Evalúo: f(-3)<0; f(-2)>0, f(-1)>0; f(0)>0;
f(1)<0, f(3)>0
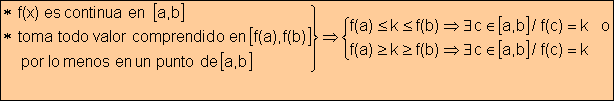
![]()
Por consiguiente, toda función continua en [a,b] está acotada
![]()
Teorema
Si
una función es continua y estrictamente creciente (decreciente) en [a,b], existe la función inversa en el intervalo
correspondiente [f(a),f(b)], que es continua y estrictamente creciente (decreciente).