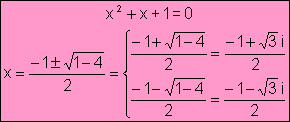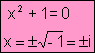POLINOMIOS
· Raíces de polinomios (Ceros de polinomios)
· Cálculo de las raíces de un polinomio. Factorización
| Temas relacionados: |
Las biografías de matemáticos son de la historia del archivo de las matemáticas en la universidad de St. Andrews, y se utilizan con el permiso.
(1765-1822)
Nació el 22 de septiembre de
1765 en Valentano, (Italia), murió el 10 de mayo de 1822 en Módena, (Italia).
Paolo
Ruffini ha sido conocido a lo largo de los años como el descubridor de la regla
que lleva su nombre, y que permite encontrar los coeficientes del polinomio
resultante de la división de un polinomio cualquiera por el binomio (x-a).
También
elaboró una demostración (que más tarde sería corregida por Abel) de la
imposibilidad de hallar la solución general de las ecuaciones algebraicas de
grado mayor o igual a cinco.
Y también en:
http://www-gap.dcs.st-and.ac.uk/~history/Mathematicians/Ruffini.html
http://www.dhistoria.com/biografias/paolo_ruffini.htm
Llamaremos polinomio real a una expresión finita de la forma:
donde:
·
·
· x:
variable o incógnita. (x es un objeto matemático llamado INDETERMINADA).
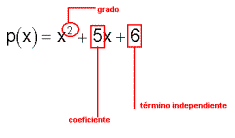
El
mayor número natural n, tal que
an¹0
se denomina grado del polinomio. Se
escribe
gr(p(x))
Ejemplo:
gr(p(x))=2
Ejemplo:
Sean dos polinomios:
gr(p(x)+q(x))=max{ gr(p(x)), gr(q(x)) }
Sea un polinomio p(x)
gr(k p(x))=gr(p(x))
Ejemplo:
gr(3 p(x))=2
Sean dos polinomios:
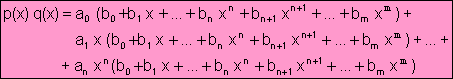
gr(p(x) q(x))= gr(p(x))+ gr(q(x))
Ejemplo:
gr(p(x) q(x))= gr(p(x))+
gr(q(x)) =2+3=5
Definiremos la potencia n-ésima de un polinomio p(x) como el polinomio obtenido al multiplicar n veces p(x) por sí mismo.
gr(p(x)n)=n
gr(p(x))
Ejemplo:
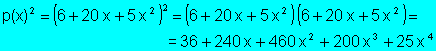
Si tenemos un cociente
de polinomios 
, se pueden presentar dos casos:
Caso A).
El grado del numerador
es menor que el grado del denominador
gr(p(x)) < gr(q(x))
Caso B).
El grado del numerador
es mayor ó igual que el grado del denominador
gr(p(x)) 
gr(q(x))
Dividir un polinomio p(x) por otro q(x) es el proceso de calcular los polinomios c(x) cociente y r(x) resto, cumpliendo:
con grado r(x) < grado q(x)
o bien el grado de r(x) es 0
Efectuamos la división polinomial:
con
gr(r(x)) < gr(q(x))
Ejemplo:
;
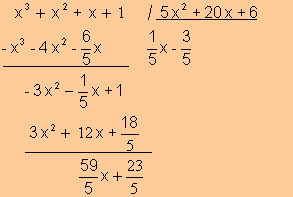
Ejemplo:
Dividimos:
En este caso r(x)= -8 x+1 q(x)=x2-x+2
Ejemplo:
Dividimos:
·
Raíces de polinomios (Ceros de polinomios)
Diremos que t es raíz
del polinomio p(x) si p(t)=0 es
decir, si al sustituir el valor de t en el polinomio y operar, el resultado es
cero. Si t es raíz, entonces el factor (x-t) dividirá al polinomio p(x) (el
resto de la división será cero).
Ejemplos:
· x = 1 es una raíz de p(x)=x2-3x+2 pues p(1)=12-3*1+2 =0
(x-1) divide a p(x)
· x = 2 es una raíz de p(x)=x2-3x+2 pues p(2)=22-3*2+2 =0
(x-2) divide a p(x)
Si un polinomio
tiene coeficientes enteros, podemos obtener las raíces enteras
del mismo entre los divisores del término independiente.
Una regla práctica
para realizar una división de polinomios es la llamada Regla
de Ruffini.
Ejemplo:
Sea x2+5x+6 . Veamos si x=2 es raíz.
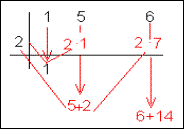
El resto será 20 (6+14), por tanto x-2 no divide al polinomio, con lo cuál seguimos probando con otro divisor del término independiente, 6, por ejemplo: -2.
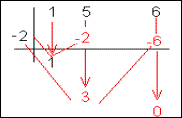
Esta vez el resto sí es cero, con lo cual (x+2) divide al polinomio. Veamos que –3 también es una raíz. Procediendo de la misma forma:
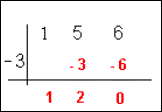
Así pues, podremos expresar el polinomio como producto de sus factores primos, proceso denominado factorización que veremos con más detalle en la próxima sección.
Ejemplo
de aplicación posterior:
En los límites con
indeterminación 
Ejemplo:
Vamos a comprobar que 
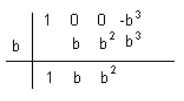
Ejemplo
q(x)= x-2
·
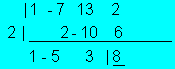
Cálculo de las raíces de un polinomio. Factorización
·
Si gr(p(x))=1 Inmediato.
Ejemplo:
p(x)=x+2 
· Si gr(p(x))=2 Aplicamos la fórmula cuadrática:
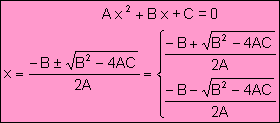
Ejemplo:
Las raíces son (aplicando la fórmula anterior): 2 y 1, y podemos factorizar el polinomio p(x) de la forma siguiente:
Nota: El polinomio del
ejemplo anterior es mónico (el coeficiente que acompaña a x2 es
la unidad). En caso de que el polinomio a factorizar no sea mónico,
multiplicaremos al factorizar por el coeficiente.
Ejemplo:
Ejemplo:
·
Si gr(p(x))=3 Aplicaremos
la regla de Ruffini, (con lo cual tendremos un polinomio de grado 2) y a
continuación la fórmula cuadrática.
·
Si gr(p(x))
Aplicaremos la regla de
Ruffini repetidamente hasta llegar a un polinomio de grado 2 y a continuación
la fórmula cuadrática.
Nota:
Cuando falla la regla de Ruffini, las raíces
pueden ser complejas.
Ejemplo:
