TRIGONOMETRÍA

 

·  Definiciones: arco, grado sexagesimal, radián, ...

· Correspondencia entre medidas

· Razones trigonométricas

· Funciones circulares o trigonométricas

· Principales fórmulas trigonométricas y su deducción

· Ángulos suplementarios, complementarios, ...

 

· Definiciones   

¿Sabías que …?

TRIGONOMETRÍA:

Deriva del griego y está compuesta por las palabras  triángulo y medida.

 

Etimológicamente significa medición de triángulos. Los elementos de un triángulo son tres ángulos y tres lados.

 

La Trigonometría estudia las relaciones entre sus medidas y el cálculo de tres de ellos conocidos los otros tres, de los cuales, uno debe ser siempre un lado. Estos estudios tienen una amplia utilización en ciencias como la Arquitectura, Astronomía, Ingeniería, etc.

 

La Trigonometría ha encontrado fácil solución a problemas como el cálculo de la altura de una montaña de cima inaccesible, la anchura de un río sin cruzarlo, el cálculo de la distancia a los planetas, …

 ARCO GEOMÉTRICO (ó circular):

Es toda porción de cicunferencia limitada por dos de sus puntos, llamados extremos. Como unidades de medida podemos destacar el grado sexagesimal y el radián.

 

ÁNGULO GEOMÉTRICO:

Es toda porción de plano limitada por un par ordenado de semirrectas llamadas lados con origen común (vértice).

La circunferencia se divide en 360 partes iguales. Cada una de ellas abarca un arco que corresponde a un ángulo de amplitud un grado sexagesimal.

El arco de amplitud un grado sexagesimal se divide en 60 partes iguales. Cada una de ellas define un ángulo de amplitud un minuto sexagesimal.

 

El arco de amplitud un minuto sexagesimal se divide en 60 partes iguales. Cada una de ellas define un ángulo de amplitud un segundo sexagesimal.

 

 

·      ÁNGULO RADIÁN:

Es una unidad de medida de ángulos. Es el ángulo central correspondiente a un radián, es decir, un ángulo que abarca un arco de longitud igual al radio de la circunferencia con que dicho arco ha sido trazado, se dice que mide un radián.

 

 ·      RADIÁN:

Es el arco cuya longitud es igual al radio de la circunferencia que lo contiene. Es una unidad de medida de arcos. 

 

  ·    CIRCUNFERENCIA GONIOMÉTRICA

   (Ó TRIGONOMÉTRICA):

 Es la circunferencia de centro el origen de coordenadas y radio unidad.

 

· Correspondencia entre medidas

(en grados sexagesimales y radianes).

Grados Sex.

 Radianes
360º 2p
180º p
90º

p / 2
60º p / 3
45º p / 4
30º p / 6

 

Ejemplo:

¿Cuántos  radianes son 12º ?

 

Efectuando una simple regla de tres:

 

Ejemplo:

¿Cuántos  grados son 2 radianes ?

 

Procediendo análogamente, y tomando p  como 3.14:

 

· Razones trigonométricas

Sea a  un ángulo orientado, con vértice en el punto A. Si tomamos un punto cualquiera B sobre un lado y desde B trazamos una perpendicular al otro lado, obteniendo el punto C, tenemos un triángulo rectángulo ABC.

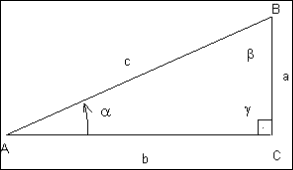
Definimos para el ángulo a  los siguientes valores llamados razones trigonométricas del ángulo a

 

Hemos definido las razones trigonométricas para un ángulo a   asociado a un triángulo rectángulo y, por tanto, un ángulo menor de 90º.

  Se puede generalizar el concepto de razón trigonométrica para cualquier ángulo.    

·        Cuadrantes y segmentos orientados

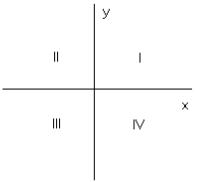
  Dos rectas perpendiculares dividen al plano en cuatro regiones, que numeramos a partir de una de ellas siguiendo el giro positivo, y llamaremos cuadrantes.

 

      Tomemos OX como origen de ángulos, es decir, dado un ángulo cualquiera a, lo trasladamos de manera que su vértice coincida con O y su primer lado con la semirrecta OX. A partir de aquí, para calcular las razones trigonométricas del ángulo a, se sigue siempre el mismo proceso:  

 

1.      Elegimos un punto cualquiera A sobre el segundo lado.

2.      Trazamos la perpendicular desde el punto elegido a la recta XX’, obteniendo el punto B.

3.      Obtenemos un triángulo rectángulo OBA.

4.      Para los signos de los catetos, se considera sobre XX’ los segmentos a partir de O. Sobre YY’ los segmentos a partir de B hacia el punto elegido A.

5.      La hipotenusa se considera siempre positiva.

 

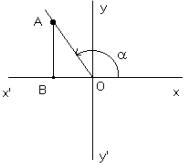
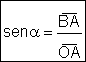
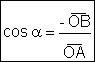
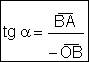
Razones trigonométricas de un ángulo situado en el segundo cuadrante

  El signo de las razones trigonométricas según el cuadrante en que se encuentre el ángulo viene expresado por el siguiente cuadro.

 

Ejemplo:

 

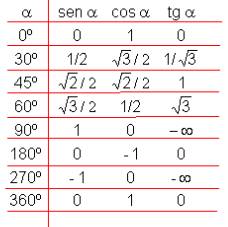
·        Resolución de triángulos

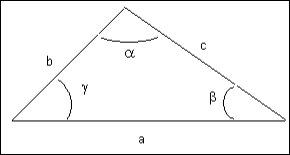
Para resolver un triángulo, necesitamos en primer lugar las siguientes  relaciones:   

·        Teorema del coseno

 

 

 

·        Teorema del seno

·        La suma de los tres ángulos es 180º

CASO 1. Dado un lado y dos ángulos.   

Ejemplo:

Resolver:

 

 

 

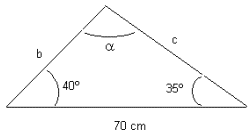
CASO 2. Dados dos lados y el ángulo opuesto a uno de ellos.  

Ejemplo:

Resolver:

 

 

 

 

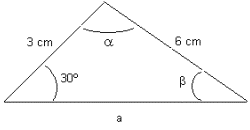
(*) Veamos 14.48º @ 14º28'48''

    Para pasar 0.48º a minutos, multiplicamos por 60 y tomamos la parte entera, es decir: 0.48 * 60 = 28.8, luego 0.48º son 28 minutos y 0.8 minutos, que razonando de la misma forma, los pasamos a segundos 0.8 * 60 = 48.

 

CASO 3. Dados dos lados y el ángulo comprendido entre ellos.

 

Ejemplo:

Resolver:

 

 

 

 

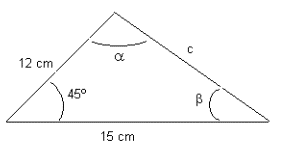
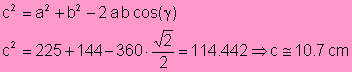
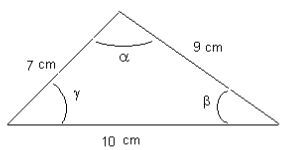
CASO 4. Dados los tres lados.

 

Ejemplo: Compobar

Resolver:

 

 

 

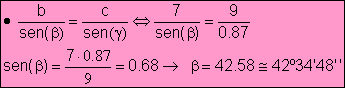
·        Resolución de triángulos rectángulos

       Si conocemos dos elementos de un triángulo rectángulo(uno de sus ángulos es 90º), (además del ángulo recto (90º)), siendo uno de ellos un lado, podremos calcular las medidas de los otros tres.

  Para resolver un triángulo rectángulo necesitamos las siguientes relaciones:

 

¨La suma de los tres ángulos es 180º

 

O lo que es lo mismo, puesto que sabemos que g = 90º

¨El teorema de Pitágoras

 

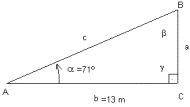
Ejemplo:

De un triángulo rectángulo se conoce el valor de un ángulo y un cateto. Halla el valor de la hipotenusa y el otro cateto.

 

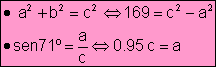
Así pues: 169 = c2 - (0.95)2c2 = c2 (0.11)

 

 

 

· Funciones circulares o trigonométricas

Son las funciones que resultan de las razones trigonométricas de un ángulo ó arco al considerar como variable independiente x, su medida en radianes.  

Ejemplos:  

 ·        La curva que representa gráficamente la función y= sen(x) se llama sinusoide.

 

 

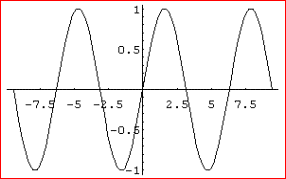
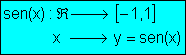
¨Es continua en Â.

¨Es periódica, de periodo 2p.

¨Es una función impar.

¨Es estrictamente creciente en

.

¨Es estrictamente decreciente en

.

 

COMPROBAR

Como la función seno es continua y estrictamente creciente en , y su conjunto de valores es [-1,1], por tanto, existe su función inversa.

y =arc sen(x)

(y es igual al arco cuyo seno es x)

 

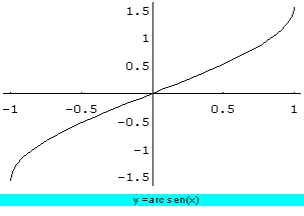
·        La curva que representa gráficamente la función y= cos(x) se llama cosinusoide.

 

 

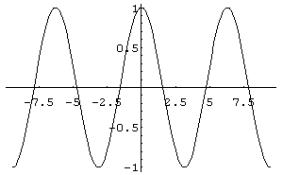
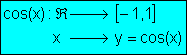
¨Es continua en Â.

¨Es periódica, de periodo 2p.

¨Es una función par.

¨Es estrictamente creciente en

.

¨Es estrictamente decreciente en

.  


  

·        La curva que representa gráficamente la función y= tg(x) se llama tangentoide.

 

 

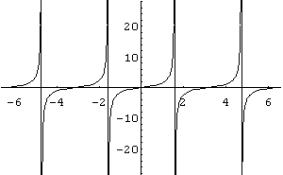
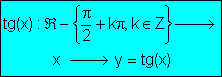
¨Es continua en todo su dominio de definición.

¨Es periódica, de periodo p.

¨Es una función impar.

¨Es estrictamente creciente en todo su dominio.  

¨

La función tangente es continua y estrictamente creciente en  y su conjunto de valores es , por tanto existe su función inversa,

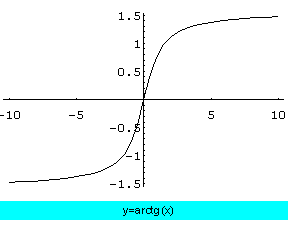
y=arctg(x)

que es continua y estrictamente creciente en , y tiene por conjunto de valores .


 

·        La curva que representa gráficamente la función y= ctg(x)

 

 

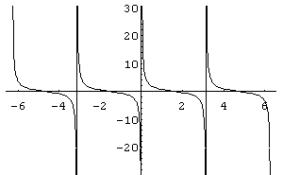
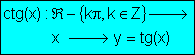
¨Es continua en todo su dominio de definición.

¨Es periódica, de periodo p.

¨Es una función impar.

¨Es estrictamente decreciente en todo su dominio.

¨

   

·        La curva que representa gráficamente la función y= sec(x)

 

 

 

 

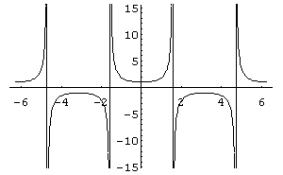
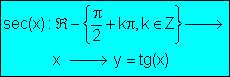
¨Es continua en todo su dominio de definición.

¨Es periódica, de periodo 2p.

¨Es una función par.

¨Es estrictamente creciente en

.

¨Es estrictamente decreciente en

.

 

¨

 

· Principales fórmulas trigonométricas y su deducción

 

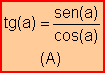
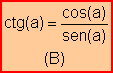
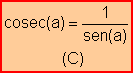
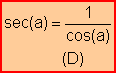
Partiendo de 

(1) tenemos:

©  Si dividimos (1) por sen2(a) y aplicamos (B) y (C)

©  Si dividimos (1) por cos2(a) y aplicamos (A) y (D)

 

Ejemplo de aplicación: Sabiendo que sen(a) = 3/17 (90º < a < 180º), halla cos(a) y tg(a). 

Por estar en el segundo cuadrante, tomaremos el signo negativo en la raíz.

 Pasamos a las razones trigonométricas de suma y resta de ángulos

(2) ® Si a=b ®

(3)

(4) ® Si a=b ®

(5)

Utilizando (A):

(6) ® Si a=b ®

(7) 

        De igual forma, o utilizando (B)

Vamos a trabajar un poco más con las relaciones (2), (3).

(2)

(3)

Si sumamos (2) y (3)

® (8)

Ejemplos de aplicación: 

   

2). Halla una solución particular de la siguiente ecuación diferencial:

 

Sol:

En primer lugar y utilizando la fórmula (8) queda:

Así pues, ensayamos con una solución del tipo:

 

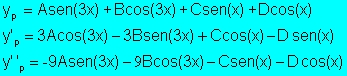
C=-3/4A=-3/20

 

Resolviendo el sistema queda A = -3/20; B = D = 0; C = -3/4

 Trabajemos ahora con las relaciones (4) y (5):

(4)

(5)

·        Si sumamos (4) y (5)

® (9)

·        Si restamos (5) y (4)

 

® (10)

· Ángulos suplementarios,  complementarios, ...    

ÁNGULOS  SUPLEMENTARIOS

 

      Llamaremos ángulos suplementarios aquellos cuya suma es 180º. Serán suplementarios 30º y 150º, 45º y 135º, 60º y 120º,...

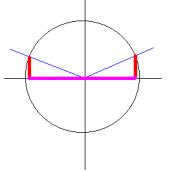
Supongamos un ángulo a / 0 £  a £ p/2.

(Pensemos por ejemplo en 30º)  

        Representemos gráficamente sus razones trigonométricas seno y coseno  en la circunferencia goniométrica (circunferencia de centro (0,0) y  radio 1); el trazo rojo será el seno y el trazo rosa el coseno.

Si representamos en la misma circunferencia el seno y coseno de su suplementario  

(En nuestro caso será 150º)

comprobamos que sus senos son iguales y sus cosenos opuestos, esto es:

Así pues, sabiendo que:  

· sen(30º) = 1/2,    deduciremos que         · sen(150º) = 1/2 

· cos(30º) = ,    deduciremos que        · cos(150º) =  

Sabiendo que:  

· sen(45º) = ,    deduciremos que         · sen(135º) =  

· cos(45º) = ,    deduciremos que         · cos(135º) =

Sabiendo que:  

· sen(60º) = ,    deduciremos que         · sen(120º) =  

· cos(60º) = 1/2 ,    deduciremos que         · cos(120º) = -1/2  

ÁNGULOS QUE SE DIFERENCIAN 180º

 

          Vamos a relacionar las razones trigonométricas de los ángulos que se diferencian en 180º, como pueden ser: 30ºy 210º, 45º y 225º, 60º y 240º,...

          

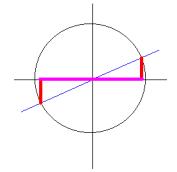
Supongamos un ángulo a / 0 £  a £ p/2.

(Pensemos por ejemplo en 30º)  

        Representemos gráficamente sus razones trigonométricas seno y coseno  en la circunferencia goniométrica (circunferencia de centro (0,0) y  radio 1); el trazo rojo será el seno y el trazo rosa el coseno.

        Si representamos en la misma circunferencia el seno y coseno de un ángulo que se diferencie de éste en 180º  

(En nuestro caso será 210º)

comprobamos que el seno del primero es igual al seno del segundo con signo opuesto y el coseno del primero es igual al coseno del segundo con signo opuesto, esto es:

Así pues, sabiendo que:  

· sen(30º) = 1/2,    deduciremos que         · sen(210º) = -1/2 

· cos(30º) = ,    deduciremos que        · cos(210º) =  

Sabiendo que:  

· sen(45º) = ,    deduciremos que         · sen(225º) =  

· cos(45º) = ,    deduciremos que         · cos(225º) =

Sabiendo que:  

· sen(60º) = ,    deduciremos que         · sen(240º) =  

· cos(60º) = 1/2 ,    deduciremos que         · cos(240º) = -1/2  

ÁNGULOS COMPLEMENTARIOS

 

            Vamos a hallar relaciones entre las razones trigonométricas de ángulos cuya suma es 90º como por ejemplo: 30º y 60º.

       

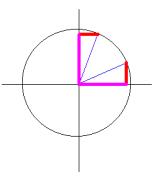
Supongamos un ángulo a / 0 £  a £ p/2.

(Pensemos por ejemplo en 30º)  

        Representemos gráficamente sus razones trigonométricas seno y coseno  en la circunferencia goniométrica (circunferencia de centro (0,0) y  radio 1).

        Si representamos en la misma circunferencia el seno y coseno de un ángulo que entre los dos sumen 90º,  

(En nuestro caso será 60º)

comprobamos que el seno del primero es igual al coseno del segundo y el coseno del primero es igual al seno del segundo, esto es:

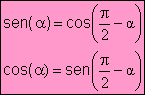
Así pues, sabiendo que:  

· sen(30º) = 1/2,    deduciremos que         · cos(60º) = 1/2 

· cos(30º) = ,    deduciremos que        · sen(60º) =   

ÁNGULOS QUE SE DIFERENCIAN 90º

 

Vamos a relacionar las razones trigonométricas de los ángulos que se diferencian en 90º, como pueden ser: 30º y 120º, 45º y 135º, 60º y 150º,...

          Supongamos un ángulo a / 0 £  a £ p/2.

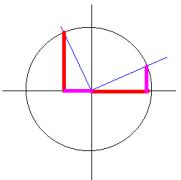
(Pensemos por ejemplo en 30º)  

        Representemos gráficamente sus razones trigonométricas seno y coseno  en la circunferencia goniométrica (circunferencia de centro (0,0) y  radio 1).

        Si representamos en la misma circunferencia el seno y coseno de un ángulo que se diferencie de éste en 90º,  

(En nuestro caso será 120º)

comprobamos que el seno del primero es igual al coseno del segundo con signo opuesto y el coseno del primero es igual al seno del segundo, esto es:

Así pues, sabiendo que:  

· sen(30º) = 1/2,    deduciremos que         · cos(120º) = -1/2 

· cos(30º) = ,    deduciremos que        · sen(120º) =  

Sabiendo que:  

· sen(45º) = ,    deduciremos que         · cos(135º) =  

· cos(45º) = ,    deduciremos que         · sen(135º) =

Sabiendo que:  

· sen(60º) = ,    deduciremos que         · cos(150º) =  

· cos(60º) = 1/2 ,    deduciremos que         · sen(150º) = 1/2

ÁNGULOS  OPUESTOS

 

Vamos a relacionar las razones trigonométricas de los ángulos que suman 360º, como pueden ser: 30º y 330º, 45º y 315º, 60º y 300º,...

              Supongamos un ángulo a / 0 £  a £ p/2.

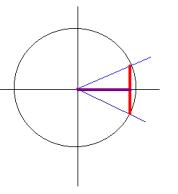
(Pensemos por ejemplo en 30º)  

        Representemos gráficamente sus razones trigonométricas seno y coseno  en la circunferencia goniométrica (circunferencia de centro (0,0) y  radio 1); el trazo morado será el coseno y el trazo rojo el seno.

        Si representamos en la misma circunferencia el seno y coseno del ángulo opuesto a éste -a =2p - a,  

(En nuestro caso será 330º)

comprobamos que el seno del primero es igual al seno del segundo con signo opuesto y el coseno del primero es igual al coseno del segundo, esto es:

Así pues, sabiendo que:  

· sen(30º) = 1/2,    deduciremos que         · sen(330º) = -1/2 

· cos(30º) = ,    deduciremos que        · cos(330º) =  

Sabiendo que:  

· sen(45º) = ,    deduciremos que         · sen(315º) =  

· cos(45º) = ,    deduciremos que         · cos(315º) =

Sabiendo que:  

· sen(60º) = ,    deduciremos que         · sen(300º) =  

· cos(60º) = 1/2 ,    deduciremos que         · cos(300º) = 1/2