Fractales matemáticos en tres dimensiones
Introducción a los fractales
La geometría fractal estudia las formas que tienen dimensión fraccionaria. Se puede creer que con las tres dimensiones del espacio se puede representar cualquier cuerpo, pero eso no es así.
Un ejemplo clásico es el de intentar medir la longitud de costa de una isla. Sobre un mapa a gran escala el perímetro tendrá un valor determinado, pero si se busca otro plano a menor escala, aparecerán tramos antes inapreciables que modificarían la longitud total. Desplazándose a la isla en cuestión, se puede intentar medir sobre las rocas dicha longitud, pero aún así no sería una medida acertada. Cada roca tiene entrantes y salientes que no podemos controlar. No digamos ya si se analiza a escala atómica.
Se llega a la conclusión que su longitud es infinita. La línea de costa es un fractal natural. Sus medidas dependen del nivel de precisión que se necesite.

Los fractales suelen caracterizarse por un elemento básico que se repite un número infinito de veces y a diferentes escalas sobre toda su extensión.
Muchos elementos de la naturaleza tienen esa estructura. Un simple árbol es un fractal, donde de un tronco inicial salen unas ramas que se descomponen a su vez en otras. También en muchas hojas podemos apreciar elementos que se repiten a diferentes escalas.
 |
 |
Con las matemáticas hemos podido entender muchos de los procesos de la naturaleza y, por qué no, también podemos intentar representar esos elementos o inventarnos otros más enigmáticos si cabe.
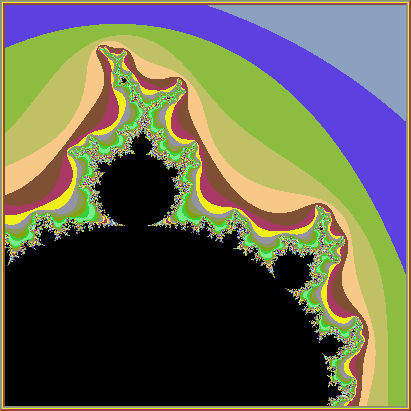
En este artículo voy a intentar que conozcáis uno de los fractales matemáticos más asombrosos que existen: “El Conjunto de Mandelbrot”.El Conjunto de Mandelbrot
De un estudio puramente matemático del comportamiento de los números complejos al aplicarles funciones iterativas (en las que el resultado de una operación sirve como base para la misma operación f(n+1)=f(n)+C), Mandelbrot ideó, hace ya más de 15 años, una representación gráfica ciertamente asombrosa, que haciendo honor a su nombre, se llamo "El Conjunto de Mandelbrot".
Ya que está basada en un conjunto infinito de números (los números complejos), la imagen es infinitamente grande, pero aplicando una serie de restricciones podemos llegar a representarla con el nivel de detalle que queramos.
Para tener una idea general de cómo se crea el conjunto gráficamente, hay que plantearse que a cada punto de la imagen le corresponde un número complejo que suele estar representado por dos coordenadas. Para que el dibujo sea proporcionado, los números asociados a cada punto se incrementan en un valor constante tanto horizontal como verticalmente.
Ejemplo: Una imagen de 4*4 pixeles con los números complejos asociados:
|
0 |
1 |
2 |
3 |
|
|
0 |
(0,0) |
(0,6) |
(0,12) |
(0,18) |
|
1 |
(6,0) |
(6,6) |
(6,12) |
(6,18) |
|
2 |
(12,0) |
(12,6) |
(12,12) |
(12,18) |
|
3 |
(18,0) |
(18,6) |
(18,12) |
(18,18) |
Cuando ya hemos realizado dicha asociación, pasamos a aplicar una función iterativa a cada punto, donde el resultado de la operación vuelve a ser tratado como entrada en la siguiente iteración de la función. Se establece un número máximo de iteraciones para que el proceso no sea infinito. Si mientras se realizan los cálculos llegamos a unos resultados determinados de antemano, el proceso se para en ese instante. El número de veces que hayamos realizado es un indicador que nos permite elegir un color determinado para ese punto.
Ejemplo: Una vez aplicada la fórmula a cada punto obtenemos los índices:
|
0 |
1 |
2 |
3 |
|
|
0 |
3 |
4 |
4 |
4 |
|
1 |
3 |
3 |
4 |
5 |
|
2 |
3 |
3 |
5 |
5 |
|
3 |
4 |
5 |
5 |
6 |
al 3 le asignamos el color azul, al 4 el rojo, al 5 el amarillo y al 6 el gris.
Existen programas que nos permiten explotar tanto este conjunto como muchos otros creados a raíz de él. Suelen partir de una vista general y gráficamente, mediante el uso del teclado o del ratón, nos permiten seleccionar un área a ampliar; el programa redibuja dicha área aumentando la resolución y nos permite volver a ampliarla nuevamente (cada vez los cálculos serán más difíciles y el tiempo de ejecución será por lo tanto mayor).
Ejemplo: Si la base de la imagen inicial es:
|
0 |
1 |
2 |
3 |
|
|
0 |
(0,0) |
(0,6) |
(0,12) |
(0,18) |
|
1 |
(6,0) |
(6,6) |
(6,12) |
(6,18) |
|
2 |
(12,0) |
(12,6) |
(12,12) |
(12,18) |
|
3 |
(18,0) |
(18,6) |
(18,12) |
(18,18) |
y queremos ampliar los cuatro pixeles del centro al tamaño inicial, deberemos dividirlos proporcionalmente:
|
0 |
1 |
2 |
3 |
|
|
0 |
(6,6) |
(6,8) |
(6,10) |
(6,12) |
|
1 |
(8,6) |
(8,8) |
(8,10) |
(8,12) |
|
2 |
(10,6) |
(10,8) |
(10,10) |
(10,12) |
|
3 |
(12,6) |
(12,8) |
(12,10) |
(12,12) |
y aplicando las fórmulas a cada punto obtendremos la nueva imagen.
 |
 |
 |
|
Base matemática del Conjunto de Mandelbrot
Sea Z un número complejo en la forma (a+bi).
Se procede a elevarlo al cuadrado y sumarle una constante C:
Z = Z^2 + C
Donde Z vale 0 inicialmente y C es un punto del plano complejo.
El resultado se vuelve a meter en la variable Z, realizando la misma operación otra vez.
En términos matemáticos se representaría con la ecuación:
Z(n+1) = Z(n)^2 + C.
Cuanto más veces se itere la fórmula, el número complejo resultante deberían hacerse cada vez mayor, pero no ocurre así en todos los casos. El parámetro que determina su crecimiento es el módulo del complejo. Si el módulo (que no es imaginario, sino real) es 2 o mayor, está demostrado que seguirá creciendo infinitamente. Sin embargo hay complejos que por mucho que los elevemos al cuadrado nunca nos darán como resultado un número complejo cuyo módulo sea superior a 2. Este conjunto de puntos definen lo que se llama "El Lago de Mandelbrot". Las "orillas" del Lago están definidas por los puntos que superan la barrera del 2 en un número infinito de iteraciones.
Para volcar el Conjunto de Mandelbrot sobre una imagen se deben seguir los siguientes pasos:
a) Se recorren todos los puntos útiles del dibujo. A cada uno de ellos se le asigna un complejo que viene determinado por una sencilla operación de correspondencia entre el plano complejo y los píxeles de la pantalla.
b) Sea el complejo C=a+bi el que corresponde a un punto determinado del dibujo. Si se aplica la fórmula anterior se obtiene otro complejo:
Z = Z^2 + C, cuya parte real e imaginaria viene dada por:
Zr(n+1) = Zr(n)^2 - Zi(n)^2 + Cr
Zi(n+1) = 2*Zr(n)*Zi(n) + Ci
c) Calcular el módulo del complejo:
|Z| = sqr(Zr^2 + Zi^2)
d) Si su valor es menor que 2, volver al paso b) y aumentar en uno un contador puesto inicialmente a cero. Este contador nos dirá cuantas iteraciones son necesarias para superar el 2.
e) Pararemos cuando el módulo del complejo sea mayor que 2 o el número de iteraciones haya superado un número determinado de veces (al que llamamos "criterio de parada").
f) Daremos un color al punto de la imagen en función del contador. Si ese contador es igual al criterio de parada consideraremos que el punto forma parte del "Lago de Mandelbrot" y le asignaremos el color de fondo.
Si la constante C fuera la misma para todos los puntos del dibujo, y no dependiera de la posición, obtendríamos los llamados "Conjuntos de Julia". Hay uno diferente para cada punto del plano complejo. Estos conjuntos están completamente relacionados con el Conjunto de Mandelbrot. Para cada punto de éste se puede decir que hay un conjunto de Julia.
Cuando el punto es significativo, es decir, cuando está situado en las orillas del Lago de Mandelbrot, el Conjunto de Julia resultante es una especie de ampliación de la zona del Conjunto de Mandelbrot.
Hay que tener en cuenta que en estos fractales hay muchas estructuras que se repiten a diferentes escalas, pero siempre con alguna diferencia más o menos apreciable.
Creación de pares estereoscópicos a partir de imágenes generadas del Conjunto de Mandelbrot
Cuando analizamos una imagen del Conjunto de Mandelbrot o de cualquier conjunto de Julia generadas a partir del algoritmo descrito anteriormente, observamos que el aspecto final nos recuerda mucho a un atractor donde hay áreas extensas que van disminuyendo en cuanto nos acercamos a los bordes del Lago de Mandelbrot. Ese detalle visual puede ser aprovechado para crear una segunda imagen con la que podamos acabar teniendo un par pseudo-estereoscópico que realce mucho más el resultado ya de por sí impresionante.
Supongamos que una línea de la imagen fractal ha sido creada partiendo del siguiente array de contadores:
|
3 |
3 |
3 |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
3 |
Si asignamos a cada contador un color:
0 -> Color A
1 -> Color B
2 -> Color C
3 -> Color D
los píxeles de la imagen tomarán los siguientes colores:
|
D |
D |
D |
C |
C |
C |
B |
B |
B |
A |
A |
A |
B |
B |
C |
C |
C |
C |
D |
D |
Entonces podemos crear una segunda imagen desplazando los colores en función del contador que representan:
|
D |
D |
C |
C |
B |
B |
A |
A |
A |
B |
B |
C |
C |
C |
C |
Por último rellenaremos los huecos:
|
D |
D |
D |
D |
D |
C |
C |
B |
B |
A |
A |
A |
A |
B |
B |
B |
C |
C |
C |
C |
El resultado puede verse en estas imagenes:
 |
 |
 |
 |
 |
|
| Preguntas, dudas, comentarios, críticas ... |  |
|
 |
||