Apéndice 2: Ecuaciones de la tangente y la normal a una curva en un punto
Casi al inicio del tema, comprobamos que “la
derivada ![]() de una función en un punto
de una función en un punto![]() es la pendiente de la recta tangente a la curva
es la pendiente de la recta tangente a la curva
![]() en el punto P
en el punto P![]() ”, y, a continuación, dimos las ecuaciones de las rectas
tangente y normal a la curva de una función
”, y, a continuación, dimos las ecuaciones de las rectas
tangente y normal a la curva de una función
![]() en un punto
en un punto ![]() .
.
No obstante, ya advertimos que en aquel momento sólo podíamos poner un ejemplo, ya que todavía sabíamos calcular funciones derivadas. Pero ahora que ya hemos aprendido a hacerlo, podemos aplicar los conocimientos adquiridos para hallar ecuaciones de rectas tangentes y normales a diferentes curvas en cualquier punto en el que su función sea derivable.
Incluso nos gustaría hacer notar al alumno con qué facilidad se pueden hallar las ecuaciones de dichas rectas, gracias al concepto de derivada de una función en un punto.
Ejemplos:
a) Hallar las ecuaciones de la tangente y la
normal a la curva de ecuación ![]() en el punto de abscisa
en el punto de abscisa
![]() .
.
Recordemos que la ecuación de la tangente era
![]()
por lo que, en este caso,
![]()
y, por otra parte,
![]() , por lo que
, por lo que
![]()
luego las ecuaciones pedidas serán:
Tangente:
![]() ®
®
![]()
Normal:
![]() ®
®
![]()
![]()
b) Hallar las ecuaciones de la tangente y la
normal a la curva de ecuación ![]() en el punto de abscisa
en el punto de abscisa
![]() .
.
En este caso,
![]() . Y, por otra parte,
. Y, por otra parte,
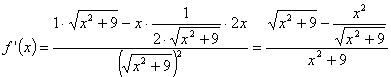
Es conveniente advertir que, como en estos casos la función derivada sólo se necesita para hallar el valor de la derivada en el punto pedido, no será necesario hacer operaciones en ella para dejarla más simplificada, ya que enseguida se va a sustituir la x por el valor dado. En este ejemplo, pues,
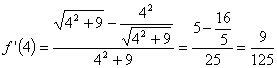
Por tanto,
Tangente:
![]() ®
®
![]()
Normal:
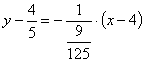 ®
®
![]()
c) Hallar las ecuaciones de la tangente y la
normal a la curva de ecuación ![]() en el origen de coordenadas.
en el origen de coordenadas.
En efecto, la curva pasa por el origen
de coordenadas, ya que ![]() . Por otra parte,
. Por otra parte,
![]() ®
®
![]()
Por tanto,
Tangente:
![]() ®
®
![]() ó
ó ![]()
Normal:
![]() ®
®
![]() ó
ó ![]()
d) Hallar las ecuaciones de la tangente y la
normal a la curva de la función ![]() en el punto de abscisa
en el punto de abscisa
![]() .
.
Por un lado,
![]() . Y, por otra parte,
. Y, por otra parte,
![]()
de donde
![]()
Por tanto,
Tangente:
![]() ®
®
![]()
Normal:
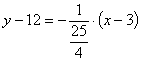 ®
®
![]()