Aplicaciones de las derivadas

    Estudio local de una función

Nota previa: Para abreviar, en lo sucesivo llamaremos h al , especifican­do a veces su signo. Vamos a estudiar una propiedades de las funciones derivables que se refieren al entorno de un punto, por lo que se llaman propiedades locales.

·  Crecimiento y decrecimiento de una función

         Sea  definida en un intervalo abierto     y sea  .

Definición 1

Diremos que la función  f  es estrictamente creciente en  c    Û   

Û    tal que, siendo    y siendo  , entonces se verifica que

es decir, si “un poco” a la izquierda de c la función toma un valor menor que en c, y “un poco” a la derecha de c toma un valor mayor que en c.

Definición 2

Diremos que una función  f  es estrictamente decreciente en  c   Û 

Û    tal que, siendo    y siendo  , entonces se verifica que

es decir, si “un poco” a la izquierda de c la función toma un valor mayor que en c, y “un poco” a la derecha de c toma un valor menor que en c.

Nota 1: Aunque somos conscientes de que ello supone una pérdida de rigor, e incluso una incorrección matemática, para facilitar los conceptos al alumno en la práctica hablaremos de función “creciente” en c cuando se den las condiciones de la definición 1, y de función “decreciente” en c cuando se den las condiciones de la definición 2.

Nota 2: El alumno debe observar que se está hablando de crecimiento o decrecimiento ¡en un punto! lo cual podría ser objetado como un absurdo o como una contradicción. Sin embargo, fijándonos bien en las condiciones de crecimiento y de decrecimiento, podemos observar que en realidad se está hablando de función creciente o decreciente “al pasar” por c.

·  Condiciones suficientes de crecimiento y de decrecimiento

Teorema:  Sea  f  definida en    y derivable en  . Entonces

           creciente en c

    decreciente en c

¨ La demostración rigurosa de este teorema requiere el conocimiento de una propiedad de los límites de funciones que puede que el alumno no conozca. Por ello, aunque hemos optado por darla a continuación, la incluimos intercalada entre dos líneas de puntos, pudiendo omitirse en una primera lectura.

..............................................................................................

  Si      y como una función llega a tomar el mismo signo que su límite,    entonces   ,  luego

            si 

            y si 

que son las condiciones para que  f  sea estrictamente creciente en c.

            Análogamente se demuestra el caso decreciente en c. x

..............................................................................................

Sin embargo, sí que podemos intentar dar una “demostración” gráfica, de tipo práctico, poco rigurosa pero intuitiva.

¨  Recordemos que  pendiente de la tangente en c.  Enton­ces como

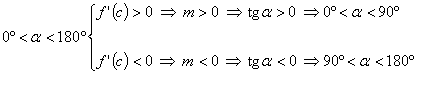
Nota importante:  El recíproco no es cierto. Es decir, una función puede ser creciente o decreciente en un punto c con .

Como contraejemplo podemos poner la función   en  , pues su gráfica, que es muy fácil de hallar, nos pone de manifiesto que es creciente en

Además, también se podría comprobar que “un poco” a la izquierda de  to­ma un valor menor que en , y “un poco” a la derecha de  toma un valor mayor que en . Y, sin embargo, como su función derivada es , en ese punto toma el valor .