Cálculo de Derivadas

Índice

Atrás

·  5.7. Derivadas de las funciones trigonométricas y ciclométricas

·  5.7.1. Derivada de la función seno                                

    En la deducción de la función derivada de la función seno, el alumno notará que se hace necesario utilizar la fórmula de transformación de una resta de senos en producto, así como el hecho de que   

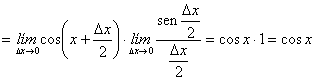
¤ “La derivada de la función seno es la función coseno”.

O, si se nos permite “abreviar” para una mayor facilidad mnemotécnica,

¤ “La derivada del seno es el coseno”

 Incluyendo la Regla de la Cadena:       

Ejemplos:

   a)  Si  

   b)  Sea , que evidentemente es una función compuesta: función seno de la función cuadrado, o, si se nos permite “abreviar”, seno del cuadrado. Su derivada será  , que, para evitar posibles confusiones en su interpretación matemática considerándola como el coseno de , deberíamos escribir, bien como , o mucho mejor como  , por la propiedad conmutativa del producto.

   c)  Sea ahora . En este caso hay que recordar claramente que, como el alumno ya debió aprender en Trigonometría, se trata de la función compuesta cuadrado del seno; es decir, que tal vez en realidad se debería escribir como , pero que en la práctica se ha adoptado la notación primera, tanto en el caso del seno como para las restantes funciones trigonométricas. Una vez aclarado esto, derivaremos aplicando la Regla de la Cadena, obteniendo:

   d)  Sea ahora , que, bien interpretada, vemos que es composición de tres funciones: es el cuadrado del seno del cuadrado. Por tanto, al derivar tendremos:

   e)  Si  , que evidentemente, es el seno del logaritmo neperiano, su derivada será

   f)  Si ,  seno de un cociente, su derivada será

   g)  Si , que indudablemente es un producto de dos funciones:   y  , que habíamos anunciado antes que volveríamos a abordar. Su derivada será

Tal vez alguien, fijándose en el logaritmo neperiano que aquí aparece, podría hacernos notar que hubiéramos podido aplicar, antes de derivar, la propiedad del logaritmo de un producto, con lo que la función hubiera quedado de entrada como

y al derivar hubiéramos tenido:

expresión equivalente a la anterior. No obstante, parece que, en este caso, el proceso de derivación no se ha hecho por ello más sencillo.

   h)  Si   estamos ante una función compuesta de tres funciones: ,  y . Es decir, que se trata del seno del logaritmo neperiano de una potencia. Si la derivamos tal como está, tendríamos:

         No obstante, podríamos haber aplicado la propiedad del logaritmo de una potencia, y escribir la función como

con lo cual, al derivarla se tiene:

resultado que claramente coincide con el anterior.

 ·  5.7.2. Derivada de la función coseno                                       

            Haciendo uso de una conocida propiedad trigonométrica, tendremos:           

¤ “La derivada de la función coseno es la función seno cambiada de signo”

         O, con expresión menos rigurosa pero más breve:

¤ “La derivada del coseno es ‘menos’ seno”

 Incluyendo la Regla de la Cadena:     

Ejemplos:

   a)  Si  , al ser producto de una constante por una función, su derivada será 

   b)  Si , al igual que vimos en el apartado anterior, se tratará de la función compuesta cuadrado del coseno, por lo que aplicando la Regla de la Cadena tendremos:

   c)  Si , se tratará del producto de una constante por una función que es función compuesta de otras tres, pues es cuadrado del coseno del cuadrado. Así pues, al derivar tendremos:

   d)  Si , hemos de fijarnos primeramente, sin que ello nos suponga ningún sobresalto, que nos hallamos ante una función compuesta de cuatro funciones: se trata del cuadrado del coseno del logaritmo neperiano de la raíz de x. Por tanto, aplicando reiteradamente con toda calma la Regla de la Cadena, obtendremos: la derivada del cuadrado, multiplicada por la derivada del coseno, multiplicada por la derivada del logaritmo neperiano, y multiplicada finalmente por la derivada de la raíz cuadrada. Es decir:

   e)  Si ,  estamos volviendo a plantearnos, como habíamos anunciado anteriormente, el derivar un cociente de funciones:  y  . Por tanto, será:

   f)  Sea . Evidentemente, se trata del producto de una constante por un producto de dos funciones compuestas: el cubo del seno y el cuadrado del coseno. Su derivada será pues

   g)  Sea .

        Consideramos este ejemplo muy importante y muy representativo para la aplicación de un “consejo” en el que hemos insistido anteriormente.

         Si, sin fijarnos más, nos “lanzamos” a derivar la función tal como nos la han dado, vemos que es el logaritmo neperiano de la raíz cuadrada de un cociente, y, como tal función compuesta de otras tres, tendríamos:

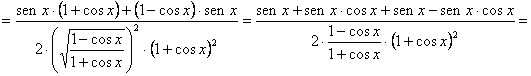
        En verdad la derivada ha quedado sumamente simplificada. Pero el proceso no podemos decir que ha sido “corto” ni “sencillo”. Al menos creemos que no tan “corto” ni tan “sencillo” como si nos hubiéramos fijado desde el principio que estábamos ante el logaritmo de la raíz cuadrada de un cociente y que, por lo tanto, antes de derivar podríamos haber aplicado las correspondientes propiedades de los logaritmos, obteniendo:

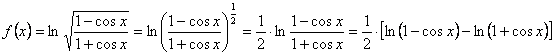
        Descompuesta así la función, su derivada será ahora:

        Evidentemente, aunque también nos ha llevado “un poco de trabajo”, el proceso de derivación ha sido más “corto” y “sencillo” que antes. En consecuencia, encarecemos al alumno que, ante ejercicios de este tipo, se fije bien en el proceso que le conviene seguir para abreviar y simplificar su trabajo.