Cálculo de Derivadas
· 5.7.3. Derivada de la función tangente
(En la
práctica se suelen tomar la primera o la tercera expresiones, es decir,
ó 
, según la que se prevea que puede convenir más para cada
ejercicio en particular).
¤ “La derivada de la tangente es igual a la unidad partida por el cuadrado del coseno”. O bien: “es igual a la unidad más el cuadrado de la tangente”.
Incluyendo la Regla de la Cadena:
Ejemplos:
a) Si
, que obviamente es una función compuesta, tangente de un
polinomio, su derivada será:
b) Si
, producto de una constante por una función compuesta
de tres funciones elementales (cubo de la tangente del cuadrado),
derivando obtendremos:
c) Sea
. Observemos que se trata de un producto de dos funciones
compuestas: raíz cuadrada del seno por logaritmo neperiano de la
tangente. Derivando, pues, como tal producto y teniendo en cuenta la Regla
de la Cadena, tendremos:
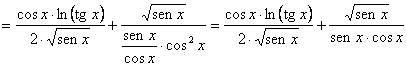
d) Sea
, obvio cociente de dos funciones sencillas. Su función
derivada será:
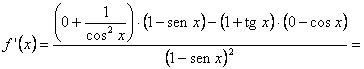
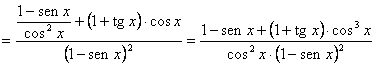
e) Sea
. Su función derivada será:
El alumno habrá observado que en este
ejemplo se ha tomado como derivada de la tangente y ello ha sido muy
“útil”, pues los cálculos han quedado sumamente sencillos. Desgraciadamente no
podemos dar un criterio general para decidir la elección de una u otra forma de
la derivada de la tangente. Sólo podemos decir que ha de ser la práctica
y la intuición las que en cada caso nos guíen para elegir una expresión u otra.
· 5.7.4. Derivada de la función cotangente
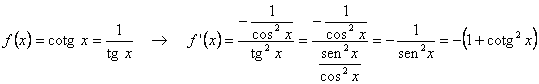
¤ “La derivada de la cotangente es igual a ‘menos’ la unidad partida por el seno al cuadrado”. O bien: “es igual a ‘menos’ la suma de la unidad con el cuadrado de la cotangente”
Incluyendo la Regla de la Cadena:
Ejemplos:
a) Si
, que evidentemente es el producto de una constante por
una función compuesta (cotangente de la mitad del cuadrado), y
recordando lo dicho anteriormente respecto a la consideración del cociente
como 
, tomaremos la función como
y procederemos a derivarla:
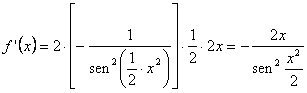
b) Si
, que manifiestamente es una función compuesta de tres
funciones (cotangente del logaritmo neperiano del cuadrado), si la
dejamos como está escrita, al derivarla tendremos:
Debemos repetir, no obstante, que, al
aparecer en la función dada 
, podríamos haber aplicado previamente la propiedad relativa
al logaritmo de una potencia y escribirlo como
. De esta manera, la función inicial quedaría
y sería ahora cotangente del producto de una constante por
logaritmo neperiano, con lo que su derivada se obtendría ahora como
ó 
c) Sea
, cociente de dos funciones que, al ser derivado como tal,
dará
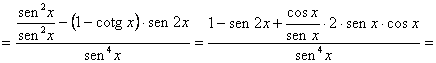
d) Sea
, producto de dos funciones, cuya derivada será:
|
|