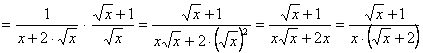Cálculo de Derivadas

Índice

Atrás

·  Caso particular: Derivada de la función raíz cuadrada  

         Ya vimos anteriormente que su función derivada es

¤ “La derivada de una raíz cuadrada es igual a la unidad partida por el doble de dicha raíz cuadrada”

Incluyendo la Regla de la Cadena:        

Nota: Como es obvio, la derivada de la función raíz cuadrada podría hallarse fácilmente como derivada de una función potencial . No obstante, dada la frecuencia con que aparece en los cálculos más diversos –y aun a riesgo de parecer contradictorios con lo dicho en el apartado anterior– consideramos muy aconsejable recordar “de memoria” su función derivada, para abreviar el trabajo.

Ejemplos:

 a)  Si          

Nota: Los ejemplos que vamos a proponer seguidamente –aparte de llevar alguna raíz cuadrada para seguir practicando su derivación– aportan en cierto modo una “novedad”, y es que se trata de funciones que son composición de tres (o más) funciones elementales “encadenadas”  para cuya derivación se seguirá la misma técnica de la Regla de la Cadena que hemos usado en tantos ejemplos anteriores, aunque reiteradamente.

Es decir que si tenemos tres funciones   ,   , y finalmente   , al derivar aplicando reiteradamente la Regla de la Cadena tendremos:

  b)  Sea . Podemos observar que se trata de la composi­ción de tres funciones elementales: ,  y . Expresado “con palabras” diríamos que es la raíz cuadrada del logaritmo neperiano de un polinomio.

         A la hora de hallar su derivada, primeramente obtendremos la derivada de la raíz cuadrada, manteniendo igual en este paso la función del radicando de la misma: . Inmediatamente a continuación multiplicaremos por la derivada del logaritmo neperiano, manteniendo análogamente igual en este paso la función sobre la cual actúa el logaritmo neperiano: . Finalmente multiplicaremos todo lo obtenido por la derivada del polinomio sobre el cual actuaba el logaritmo neperiano: .

         Resumiendo:

   c)  Sea , que también es una composición de tres funciones elementales. Expresada “con palabras” diríamos que se trata del logaritmo decimal de la raíz cúbica de un polinomio.

         Tengamos en cuenta que, habiendo aconsejado anteriormente transformar las raíces de índice mayor que dos en potencias de exponente fraccionario, en este caso antes de derivar habremos de expresar en esta forma potencial la raíz cúbica que en ella aparece. Antes de derivar escribiremos, pues,  . Y seguidamente derivaremos mediante aplicación reiterada de la Regla de la Cadena, como en el ejemplo anterior:

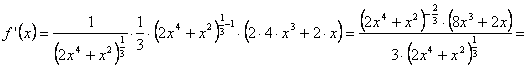
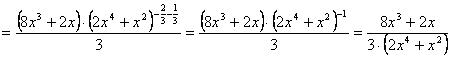
         Anteriormente comentamos, respecto al ejemplo , que “se podía” aplicar primero la propiedad del logaritmo de una potencia, con lo que se simplificaba un poco el cálculo de su derivada. Pero ahora, en el ejemplo que acabamos de poner –y naturalmente en todos aquellos casos en los que se puedan aplicar propiedades matemáticas que simplifiquen los cálculos– habremos de decir que, no sólo “se puede”, sino que “se deben” aplicar dichas propiedades para una mayor simplicidad y rapidez en el trabajo.

         Así, en este caso, antes de derivar debemos escribir:

         Con lo que ahora, al derivar, tendremos:

cálculo que, en cuanto a sencillez, no admite comparación con el realizado anteriormente. Téngase, por tanto, en cuenta este “consejo”, si se quiere ganar en rapidez y facilidad en muchos ejercicios.

   d)  Sea. Si la tomamos tal como está se trataría de una composición de tres funciones: la raíz cuadrada de la raíz cuadrada de una potencia. Si no nos fijamos más y nos lanzamos a derivarla como función compuesta, tendríamos:

No obstante, si nos fijamos bien antes de derivarla, vemos que fácilmente se puede expresar como una función potencial simple:

y, por tanto, su derivada es inmediata:

   d)  Sea  . Después de las explicaciones de los casos precedentes, consideramos que el alumno podrá seguir ya fácilmente los pasos de su derivación: