Unidad 2. Indicadores de Propiedades Resistentes
2- Ensayo de Tracción
Anterior                                                     Siguiente
2.1 LA ZONA ELÁSTICA
Se denominada zona elástica a la fracción del ensayo en la que se establece una correlación lineal, o cuasilineal, entre las tensiones axiales s y las deformaciones unitarias e.

En la figura 2.6, la zona comprendida entre las tensiones 0 y Le mantiene una correlación lineal y directa entre tensiones, s, y deformaciones, e, de tal modo que podemos expresar aquella por el modelo:

 s = E e            (2. 4)

sólo válido en el campo 0 < s < Le.
Los valores medidos, para el acero AE 235 son:

0 < s < 235 N/mm2

El campo de tensiones en el que se cumple la correlación lineal s = E e es el campo elástico. Este constituye la base para el cálculo de elasticidad.

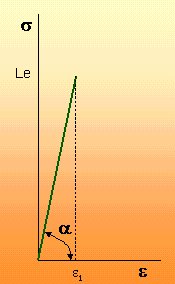
Figura 2.6. Diagrama de la zona elástica.
2.1.1 Determinación del limite elástico

El límite superior del campo elástico se le denomina límite de elasticidad o límite elástico, Le. 
El valor medido para el límite elástico en el acero ensayado es:

                     Le = 24 Kgf/mm2 = 235 MPa

El límite elástico es el límite máximo hasta donde es válida la teoría de la elasticidad.
 
2.1.2 Definición del módulo de elasticidad, E.

La característica observada en el ensayo parcial de tracción hasta los 15 kN es, además de la indicada anteriormente sobre la correlación lineal entre cargas F y alargamientos DL, la recuperación de la deformación DL cuando descienden las cargas al valor nulo. 
Es sin duda la propiedad que identifica el campo elástico.
 

En el campo elástico la correlación lineal entre tensiones, s, y deformaciones, e, se conserva también en el sentido de disminución de cargas.
 

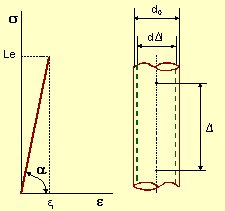
Figura 2.7. a) Definición del módulo de elasticidad o de Young. 
b) Variaciones dimensonales.
  Se define el módulo de elasticidad, E, o de Young, como el factor numérico que relaciona las tensiones, s, y las deformaciones, e, en el campo elástico. De la expresión 2.4 se deduce:

 E = s / e = tg a                             (2.5)

Los valores medidos de E en los ensayos, figura 2.7, son los siguientes:

s = 1500 Kg/78.5 mm2 = 19.1 Kg/mm2
e = 0.045/50 = 9 · 10-4
E = 19.1/9 · 10-4 = 21222 Kg/mm2 = 208190 MPa

El módulo de elasticidad, E, es un parámetro básico en teoría de elasticidad, pues cuantifica las tensiones, de difícil medición, a partir de las deformaciones, que pueden medirse sin excesiva dificultad.

El módulo de elasticidad, E, es el fundamento de la extensometría o técnica que investiga las tensiones de las piezas en servicio a partir de las deformaciones.
 
2.1.3 El coeficiente de Poisson

El coeficiente de Poisson, n, nos evalúa la relación entre la contracción relativa de una sección transversal y el alargamiento relativo de la sección longitudinal. Éste viene definido por la relación:


(2.6)

Los valores medidos en los ensayos serán:

(e)15 kN = 0.045 mm / 50 mm = 9 x 10-4
 De = (5.5 - 5.4985) / 5.5 = 2.7 x 10-4

Luego el coeficiente de Poisson será:

n  = 2.7 x 10-4 / 9 x 10-4 = 0.30

El coeficiente de Poisson es un indicador de la contracción transversal cuando la probeta se alarga longitudinalmente. El coeficiente de Poisson es parámetro básico en la teoría de elasticidad cuando se restringen los alargamientos transversales.

  

 
Menú Principal
Menú Unidad 2
Arriba