
 |
| 2.3 TENSIÓN Y DEFORMACIÓN REALES |
| La disminución
en la tensión necesaria para continuar la deformación una
vez superado el máximo, punto m de la figura 2.4, parece indicar
que la resistencia a la deformación plástica disminuye. Pero,
en realidad, ocurre todo lo contrario. No obstante, el área de la
sección disminuye rápidamente dentro de la estricción,
que es donde ocurre la deformación. Esto produce una disminución
en la capacidad de la probeta para soportar una carga. La tensión,
se obtiene con el área de la sección inicial antes de que
el material comience a deformarse, sin tener en cuenta la disminución
de área de la estricción.
En ocasiones tiene más sentido utilizar curvas de tensión-deformación reales. La tensión real sT se define como la carga dividida por le área de la sección instantánea Ai sobre la cual ocurre la deformación (por ejemplo, la estricción, una vez pasado el máximo), o sea, sT = F / Ai (2.21) Además en ocasiones también es más conveniente representar la deformación real eT, definida por eT = ln ( li / l0) (2.22) Si no ocurre cambio de volumen durante la deformación, o sea, si Ai li = A0 l0 (2.23) |
| Las tensiones y deformaciones
reales están relacionadas con las nominales mediante:
sT
= s
( 1 + e)
(2.24 a)
Estas ecuaciones ante-riores son válidas solamente al comienzo de la estricción; a partir de este punto la tensión y la deformación reales deben ser calculadas a partir de las medidas de las cargas, secciones transver-sales y longitudes de prueba reales. En la figura 2.12. se comparan las curvas de tracción nominales (o de ingeniería) con las reales. |
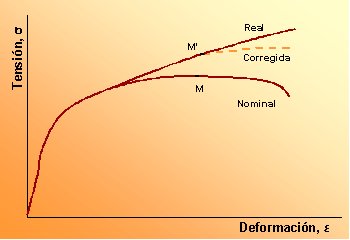
Figura 2.12. Comparación de las curvas típicas de tracción nominales (también denominadas de ingeniería) y reales (también denominadas verdaderas). La estricción empieza en el punto M en la curva nominal, lo cual corresponde al punto M’ sobre la curva real. |
| Nótese que la
tensión real necesaria para aumentar la deformación continúa
aumentando una vez superado el punto M’.
Coincidiendo con la formación de la estricción se origina un estado complejo de tensiones en la zona (es decir, existen otras componentes de la tensión además de la axial). Por consiguiente, la tensión axial correcta en la región de la estricción es ligeramente menor que la calculada a partir de la carga aplicada y del área de la sección de la estricción. Esto conduce a la curva corregida de la figura 2.13. En algunos metales y aleaciones, la región de la curva real tensión-deformación más allá del límite elástico hasta el punto en que comienza la estricción puede aproximarse mediante sT = K eTn (2.25) En esta expresión K y n son constantes, cuyos valores varían de una aleación a otra, y también dependen de las condiciones del material (o sea, de si ha sido deformado previamente, o tratado térmicamente, etc.). El parámetro n es a menudo denominado exponente de endurecimiento por deformación y tiene un valor menor que la unidad. En la tabla 2.1. se dan los valores de K y n para aleaciones. |
|
|
|
|
|
| Acero de bajo contenido en carbono (recocido) |
|
|
|
| Acero aleado (Tipo 4340 de AISI, recocido) |
|
|
|
| Acero inoxidable (Tipo 304 de AISI, recocido) |
|
|
|
| Aluminio (recocido) |
|
|
|
| Aleación de aluminio (Tipo 2024, tratada térmicamente) |
|
|
|
| Cobre (recocido) |
|
|
|
| Latón ( 70 Cu – 30 Zn, recocido) |
|
|
|
|
|
|
|
 |