
 |
| 3.4 TIPOS PRINCIPALES
DE REDES CRISTALINAS
Las redes cristalinas nos las encontramos, obligatoriamente, en materiales cerámicos y metálicos, y con menos profusión en los orgánicos. |
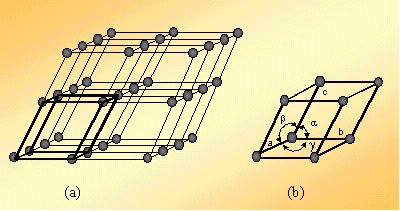
Figura 3.33. a) Retículo espacial de un sólido cristalino ideal. b) celda unidad con las constantes reticulares. |
| El ordenamiento atómico en sólidos cristalinos puede representarse asimilando los átomos a los puntos de intersección de una red de líneas en tres dimensiones. Tal red se llama retículo espacial, figura 3.33a, y puede ser descrita como una disposición de punto tridimensionalmente infinita. Cada punto de la red espacial tiene idéntico entorno y puede ser descrito por una disposición espacial mínima denominada celda unidad, figura 3.33b. |
Tabla 3.3. Clasificación de celdas unitarias.
|
Cristalino |
ángulos interaxiales |
|
|
|
a = b = c, a = b = g = 90º |
Cúbico simple
Cúbico centrado en el cuerpo Cúbico centrado en las caras |
|
|
a = b c, a = b = g = 90º |
Tetragonal sencillo
Tetragonal centrado en el cuerpo |
|
|
a b ? c, a = b = g = 90º |
Ortorrómbico simple
Ortorrómbico centrado en el cuerpo Ortorrómbico centrado en las bases Ortorrómbico centrado en las caras |
|
|
a = b = c, a = b = g ? 90º |
Romboédrico simple |
|
|
a = b ? c, a = b = 90º, g = 120º |
Hexagonal sencillo |
|
|
a ? b ? c, a = b = 90 ? g |
Monoclínico simple
Monoclínico centrado en la base |
|
|
y sin formar ningún ángulo recto, a ? b ? c, 90º, abg 90º |
Triclínico simple |
| La celda unidad se describe
por los parámetros reticulares a, b y c, y sus ángulos de
orientación a b
y g. Todas
las redes cristalinas pueden encuadrarse en 14 celdas unitarias estándar
que se indican en la tabla 3.3, y se representan en la figura 3.34.
Por su mayor interés en materiales metálicos, se describen las celdas hexagonales y cúbicas. |

Figura 3.34. Representación de las celdas unitarias. |
| 3.4.1 Hexagonal
compacto ( h.c.)
|
| Posee una sucesión
regular de planos densos del tipo ABABABA..., o BCBCB..., o CACAC... como
puede observarse en la figura 3.35c. Esta estructura se describe corriente-mente
por su retículo unidad en el que cada punto representa el centro
de la posición ocupada por un átomo. La celdilla queda descrita
por los parámetros a y c. La dirección densa, situada en
el plano basal, es la que pasa por el centro. El radio del átomo
viene determinado en esta dirección según el modelo de esferas
duras, por ra = a/2.
Con este modelo, la relación c/a debe ser 1,633, aunque con frecuencia encontramos valores aproximados que corresponden a estructuras deformadas como se observa en la tabla 3.4. |
Tabla 3.2. Energías y longitudes de enlace covalentes.
|
|
|
interatómica (Å) |
Axial |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
cc |
3.13 |
|
867 |
|
|
|
|
||
|
|
|
|
||
|
|
ccc |
2.58 |
950 |
|
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
cc |
2.89 |
|
900 |
|
|
|
|
||
|
|
|
|
| El número de coordinación,
que se define como el número de átomos que contactan con
cada uno, es en esta estructura de doce; y el número de átomos
por celdilla es de seis.
3.4.2 Cúbico centrado en caras ( c.c.c.) Posee una sucesión
regular de planos densos del tipo ABCABCABC... Esta sucesión, así
como la descripción de la celdilla unidad, puede observarse en la
figura 3.52b. Esta celdilla es descrita por solo un parámetro: el
lado del cubo a.
3.4.3 Cúbico centrado ( c.c.) Esta estructura no está construida con planos densos, por lo tanto, posee menos densidad atómica que la hd y c.c.c. La representación de la celdilla unitaria se observa en la figura 3.35a. Igualmente que en el c.c.c. el parámetro a, lado del cubo, define la celdilla. Su número de coordinación es solo ocho, pero en cambio tiene otros seis átomos a distancia poco mayor que la interatómica. La dirección densa del sistema (c.c.), es la diagonal del cubo. Por tanto, el radio del átomo vendrá expresado por: En la tabla 3.4, relacionamos
los tipos de estructuras cristalinas y parámetros característicos
de la celdilla unitaria correspondientes a los metales más usuales.
Se observará que algunos poseen dos tipos de estructura diferentes,
como es el caso del Co y Fe: corresponden a formas alotrópicas diferentes
de cada metal. Se denomina alotropía a la propiedad que presentan
algunos metales de existir, en estado sólido, conformando diferentes
estructuras a temperaturas específicas, de modo que la transformación
se realiza de forma reversible y a una temperatura definida.
3.4.4 Notaciones cristalográficas En una red cristalina, un plano cristalográfico es el que contiene diversos centros de átomos de la red. Puesto que la estructura cristalina se repite uniformemente en todas las direcciones, todos los planos paralelos que contengan la misma distribución de átomos corresponderán al mismo plano cristalográfico. Una forma usual de identificar los planos cristalográficos es mediante los índices de Miller, que poseen la ventaja de poderse utilizar directamente en análisis mediante rayos X. Para el caso de redes cúbicas, la determinación de los índices de Miller se realiza, de acuerdo con la figura 3.36, con el siguiente proceso: 1. Se trazan los ejes de referencia cartesia-nos (x, y, z) coincidentes con los parámetros de una celdilla estructural. 2. Se determinan las intersecciones del plano con los ejes de referencia cuantificadas en unidades del parámetro característico. Ver figura 3.33, en cuyo ejemplo será: 3. Se determinan sus recíprocas reducidas al mínimo común denominador.ejes x y z Recíproco genérico 1/x1 1/y1 1/z1 ejemplo 1/2 1/3 1/1.
En definitiva, los índices de Miller de un plano cristalográfico son los menores números enteros proporcionales a los recíprocos de las intersecciones del plano a los ejes cristalográficos, expresados en unidades del parámetro respectivo. |
| Así, el símbolo
(h,k,l) representa la totalidad de los planos paralelos, familia de planos
al de los índices que hemos calculado.
Si se desea indicar todos los planos cristalinos de un determinado tipo, prescindiendo de su orientación, se expresan los índices de Miller de cualquier plano de ellos encerrados en unas llaves, en la forma {h, k, l}. Este símbolo representa las familias de planos (h, k, l), (h, k, l), (h, k, l) y (h, k, l); donde h representa a -h. En la figura 3.37 se observan diversas familias de planos cristalográ-ficos denominadas por índices de Miller. |
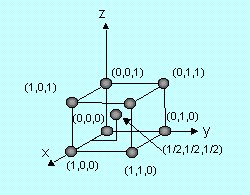
Figura 3.36. Determinación de los índices de Miller en las redes cúbicas. |
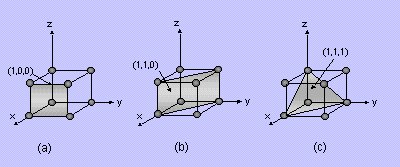
Figura 3.37. Indices de Miller de diferentes planos cristalográficos en redes cúbicas. |
| Para definir la dirección cristalográfica se traza una línea en dicha dirección que pase por el origen. Los índices de cada dirección corresponde a los índices vectoriales expresados en unidades de parámetros reticulares, tal como se representa en la figura 3.38. Por ejemplo, en el caso de un cubo su diagonal tendrá el índice [1, 1, 1]. Todas las direcciones que contengan cualquier combinación en signo + o - de los índices de aquella dirección representan la misma dirección, pertenecientes a la misma familia. La familia de índices se representa encerrada entre los los signos < y >; por ejemplo, <1, 1, 1>. |
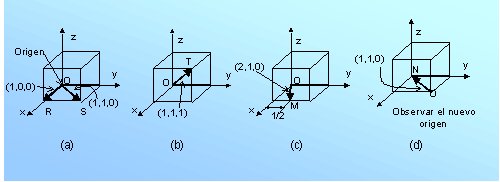
Figura 3.38. Direcciones cristalogáficas en celdas unitarias cúbicas |
|
|
|
|
 |