
 |
| Propiedades
mecanicas justificadas por la estructura cristalina
Algunas propiedades de
los metales y cerámicas pueden predecirse o justificarse mediante
la estructura cristalina perfecta, tal como se ha descrito. Es el caso
de las que se especifican a continuación:
Sin embargo, otras propiedades
no pueden ser justificadas por la estructura cristalina, porque dependen
de las desviaciones que los cristales reales presentan con respecto al
cristal ideal perfecto, entre éstas se encuentran las que se citan
en el apartado 7: plasticidad y su entorno, límite elástico,
carga de rotura, resistencia a la fluencia, resistencia a la fatiga, etc.
6.1 DENSIDAD La densidad de un metal puede deducirse a través del modelo de esferas duras, por medio del conocimiento del volumen de la celdilla, v, de la masa de cada átomo, m, y del número de átomos, n, existentes en cada celdilla. Así pues la densidad, r viene definida por: r = m . n / v (3.20) donde m se puede estimar a partir del número de Avogadro, N, y el peso molecular del metal, Pm, en la forma:
6.2 MODULO DE ELASTICIDAD Las propiedades elásticas se determinan por la fuerza necesaria para producir un cambio unitario en la forma de una probeta, y se calculan como la relación de las tensiones (s) a las deformaciones resultantes (e). En el caso de admitir su linealización, se puede representar por la pendiente de la curva en el entorno del punto de equilibrio a0 en la curva F = f (x) de las fuerzas interatómicas, figura 3.26. Así pues, el módulo de elasticidad E viene definido por: (3.22) y establece la modelización de la ley de Hooke. Con el mismo criterio podría deducirse el modulo de cizallamiento (Et) si la curva de la figura 3.26 se refiriera a fuerzas de cortadura (Fc) que tienden a hacer deslizar unos planos cristalográficos sobre sus vecinos un ángulo definido por G. Es decir: (3.23) 6.3 PUNTO DE FUSIÓN |
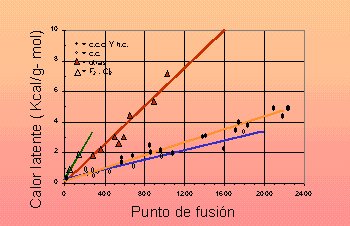
Figura 3.445. Calor latente de fusión en función de las temperaturas absolutas de fusión para varios metales. |
El punto de fusión
de un metal es la temperatura a la que se encuentra en equilibrio con la
forma líquida.
En este punto las energías potenciales de ambas formas son similares, y sus energías cinéticas muy distintas, por causa del movimiento caótico de los átomos que no fijan su posición con la ordenación característica del cristal. El calor latente de fusión es representación de la diferencia entre estas energías cinéticas entre la fase líquida y sólida. De otro modo el calor latente está correlacionado con el paso de energía interna, que se ha referido en la figura 3.29, ubicado a la distancia de equilibrio a0. |
| Según el modelo de Einstein, el átomo incrementa su amplitud de vibración de acuerdo con el aumento de la tempe-ratura hasta el punto en que la energía de vibración supera el citado pozo de energía. Por ello aparece una correlación direc-ta y lineal entre los calores latentes y temperaturas de fusión para todos los metales, tal como se observa en la figura 3.45. |
|
|
|
|
 |