Problema 4.1
Un material metálico sometido a un nivel de acritud dado recristaliza completamente en 1 hora. Calcular el grado de recristalización, para idénticas condiciones de acritud previa y temperatura, que se tiene a los 30 minutos.
Notas: La recristalización sigue un modelo de Avrami. Se supone el material completamente recristalizado para un 95% de recristalización. No se considera el tiempo de alivio de tensiones

 Problema 4.2
Experimentalmente se ha comprobado que una aleación de cobre para conductores eléctricos con una acritud del 60% recristaliza en 150 horas a 88°C, y en 200 minutos a 135°C. Se supone que el material recristaliza siguiendo un modelo de Avrami, donde para una recristalización del 95%
Determinar:
a) La energía de activación Q del proceso.
b) La constante Ct del proceso, supuesto que el factor n = 2.
c) El tiempo necesario para que el material recristalice, con idéntica acritud Ac = 0.60, a 25°C.
d) La temperatura de recristalización a 1 hora, considerando una acritud previa del 50% (Ac = 0.5).
Nota: Cte de los gases R = 8.314 J/mol K

 Problema 4.3
La figura expresa la correlación entre el tamaño de grano recristalizado y el grado de deformación plástica en laminación, medida en porcentaje de reducción de sección (% Ac). Determina, para un tamaño de grano inicial de 0.15 mm, el rango de las reducciones de sección que produce un incremento de este tamaño de grano.
 

 Problema 4.4
Una barra cilíndrica de una aleación Cu-5%Zn tiene un diámetro inicial de 6 mm y es deformada en frío, mediante trefilado, hasta un diámetro final de 5 mm. Calcular:
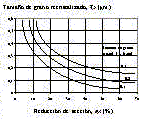
 a)  El porcentaje de deformación en frío necesario, expresado como la estricción del material.
 b)  Para esta deformación, la carga de rotura es de 455 MPa. Calcular el límite de elasticidad sabiendo que el índice general es de 0.85.
 c)  Suponiendo que el material recristaliza siguiendo el modelo de Avrami donde, para una recristalización del 95%, tenemos

 
calcular la constante Ct del proceso, si el material recristaliza en 200 minutos a 380°C (suponiendo n = 2) y considerando:
Q = 95 kJ/mol y R = 8.314 J/mol-K.
 d)  Industrialmente se considera el tiempo óptimo de recristalización de 1 hora. Si la temperatura máxima de trabajo no puede superar los 360°C, ¿cual debería ser la acritud previa que podría suministrarse al material?.
 e)  En las condiciones de acritud obtenidas en el apartado anterior, estimar el valor de carga de rotura, considerando que en estado recocido la carga de rotura de esta aleación es de 318 MPa. Suponer evolución lineal de las propiedades mecánicas en todo el rango de acritud.


 Problema 4.5
Una probeta no deformada de una aleación de cobre, tiene un diámetro medio del grano de 0.4 mm. Se le pide que reduzca el tamaño del grano a 0.2 mm. Considerando las gráficas siguientes, analizar si es esto posible, y si lo es:
 a)
Explicar los procedimientos que se utilizarían y el nombre de los procesos involucrados.
 b)
Temperatura de recocido de recristalización.
 c)
Carga de rotura alcanzada por la aleación trás la deformación en frío.

 

 

 

Tamaño grano recristalizado vs resistencia a tracción 

Temperatura de recristalización vs reducción de sección 

Resistencia a tracción vs reducción de sección 

 Problema 4.6
Si precisamos 100 horas para recristalizar completamente una lámina de aleación Al-Mg a 253°C y 8 h a 282°C, calcular para este proceso la energía de activación en kilojulios por mol. Suponer un modelo de comportamiento de velocidad de cristalización del tipo:

 

 Problema 4.7
Si para recristalizar el 50 por 100 de una pieza de cobre puro se tarda 9 minutos a una temperatura de 135°C y 200 minutos a 88°C. ¿Cuántos minutos se requerirán para recristalizar la pieza al 50 por 100 a 102°C?

 Problema 4.8
Considerando las propiedades mecánicas del cobre puro representadas en la figura, se desea obtener una barra con al menos 415 MPa de carga de rotura, 380 Mpa de límite de elasticidad, y un 5% de alargamiento. ¿Cual deberá ser la deformación en frío que debamos proporcionarle?

 Problema 4.9
Observando los datos de la tabla siguiente, determinar las temperaturas a la que se inicia la etapa de restauración, recristalización, y crecimiento de grano en un latón Cu - 12.5% Zn.

 Temperatura de recocido (°C)

 Tamaño de grano (mm)

 Carga de rotura (Mpa)

 Alargamiento (%)

 Conductividad eléctrica

25
100
150
200
250
300
350
400
500
600
700

0.100
0.100
0.100
0.100
0.100
0.005
0.008
0.012
0.018
0.025
0.050

550
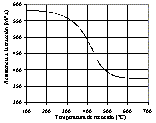
550
550
550
550
515
380
330
275
270
260

  5
5
5
5
5
9
30
40
48
48
47

16
16
17
19
20
20
21
21
21
22
22
 

 Problema 4.10
Un alambre de 5 mm de diámetro, de monel 400 (aleación de níquel), recubierto de una pequeña capa de óxido de 100 nm, sostiene un peso de 4000N, en el interior de un horno a 600°C, donde sufre una corrosión cuya velocidad cumple la ley parabólica y2 = C1·t + C0, sabiendo que con una hora de exposición su capa de óxido aumenta a 200 nm, calcular:
 a)
El tiempo en el cual iniciaría la deformación plástica.
 b)
El tiempo en el cual se produce la rotura.

Las propiedades mecánicas del monel 400 son:
Módulo de elasticidad, E = 179 GPa
Límite elástico, Le = 283 MPa
Carga de rotura, R = 579 MPa
Alargamiento hasta rotura = 39.5 %

 Problema 4.11
Sobre un latón comercial, se realiza un tratamiento de recocido para obtener una resistencia a la tracción 430 MPa, representándose en la figura a) la evolución de las características mecánicas con la temperatura de recocido. En la figura b) se representa la influencia del tamaño en las características mecánicas de esta misma aleación.

 

 

 a)

b) 
Se pide:
 a)
Estimar la temperatura a la que debería realizarse el tratamiento térmico de recocido de recristalización.
 b)
Si la evolución del tamaño de grano, durante el tratamiento de recocido, viene expresada por:

 
Donde Q = 95 kJ/mol, R = 8.314 J/mol-K, T la temperatura de recocido, k una constante del material = 0,62 cuando el tamaño de grano se expresa en mm y el tiempo de recocido, t, en segundos. Calcular el tiempo de recocido requerido si partimos de un tamaño de grano de 0,012 mm.
c)  ¿Cuál debe ser el diámetro de una barra de este material para poder soportar, sin romper, esfuerzos de 12 kN.

 Problema 4.12
El tratamiento de sinterización de microesferas de Ti en una prótesis de cadera realizada en una aleación Ti-6Al-4V, se realiza a 1250 ºC durante 2 horas. Si se parte de un tamaño de grano de 0,014 mm de diámetro equivalente, éste pasa tras el tratamiento a un diámetro de 0,32 mm.
Considerando la ecuación

 
donde Q = 107 kJ/mol y R = 8,314 J/mol-K.
 a)
¿Cuál sería el tamaño de grano resultante si se realizara el tratamiento durante sólo una hora?
 b)
¿A que temperatura se consigue un tamaño de grano de 0,32 mm con tan solo una hora de tratamiento?

 Problema 4.13
El tratamiento de sinterización
 
 

 Problema 4.14
El tratamiento de sinterización