n·p = n_i²

Para el caso de un semiconductor puro, las concentraciones de electrones y huecos son iguales, de modo que,

n = p = n_i = 1,5·10¹⁶ m^-3

b) Debido a que la concentración de impurezas es mucho más grande que la concentración intrínseca, y puesto que el arsénico es un átomo donador para el silicio, la concentración de electrones es aproximadamente igual a la concentración de impurezas:

n » 5·10²⁰ m^-3

y aplicando la ley de acción de masas la concentración de huecos será,

c) En este caso, puesto que el indio es una impureza aceptora para el silicio, tenemos:

p » 2·10²⁰ m^-3

d) Al igual que en el apartado a), para el caso de un semiconductor puro, las concentraciones de electrones y huecos son iguales a la concentración intrínseca a la temperatura indicada, de modo que,

n = p = n_i = 3,7·10²⁰ m^-3

e) En este caso, la aproximación utilizada en los apartados b) y c) no puede ser usada debido a que la concentración de impurezas no es mucho más grande que la concentración intrínseca. Por ello, junto a la ley de acción de masas habrá que utilizar también la ley de neutralidad eléctrica:

N_D + p = N_A + n

donde N_D y N_A son respectivamente las concentraciones de impurezas donadoras y aceptoras. En este caso, puesto que el arsénico es una impureza donadora tendremos que N_A = 0, y N_D = 5·10²⁰ m^-3

De este modo tenemos un sistema de dos ecuaciones con dos incógnitas,

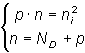
cuya solución viene dada por,

n = 6,97·10²⁰ m^-3

p = 1,97·10²⁰ m^-3

f) En esta situación, puesto que el indio es una impureza aceptora tendremos que N_D = 0, y N_A = 2·10²⁰ m^-3.

n = 2,83·10²⁰ m^-3