
VARIABLE COMPLEJA ELEMENTAL
· Formas de expresión de un número complejo
· Fundamentos de los complejos
· Raíces de ecuaciones polinómicas
· Potencias de base y exponente complejo
|
Temas relacionados: |
Abraham
de Moivre
Nato:
el 26 de mayo de 1667 en Vitry (cerca de París), Francia
Muerto: el 27 de nov de 1754 en Londres, Inglaterra
De
Moivre inició el desarrollo de la geometría analítica y de la teoría de la
probabilidad . Él publicó la doctrina de la ocasión en 1718. La definición
de la independencia estadística aparece en este libro junto con muchos
problemas con los dados y otros juegos. Él también investigó la estadística
de la mortalidad y la fundación de la teoría de anualidades.
En
Miscellanea Analytica (1730) aparece fórmula de s de Stirling el ' (atribuido
incorrecto a Stirling ) que de Moivre utilizó en 1733 derivar la curva normal
como aproximación al binomial. En la segunda edición del libro en de 1738
Moivre da crédito a Stirling para una
mejora
al fórmula.
Recuerdan a De Moivre también para su fórmula para (lechuga romana x + pecado de i x) n la cuál tomó la trigonometría en análisis.
A pesar de la eminencia científica de Moivre su renta principal estaba por
matemáticas del curso particular y é murió en pobreza. Él,
como
el cardán , es famed para predecir el día de su propia muerte. Él encontró
que él dormía 15 minutos más de largo cada noche y de esto la
progresión aritmética , calculada que él moriría en el día que él durmió
por 24 horas. ¡Él tenía
razón!
Todos
conocemos el cuerpo de los números reales: R,
que
fue creado ante la necesidad de calcular exactamente ![]() , ya que el conjunto Q
de
los números racionales era insuficiente.
, ya que el conjunto Q
de
los números racionales era insuficiente.
Ahora
bien, en este conjunto R,
no se puede calcular exactamente, por ejemplo ![]() , pues no existe ningún número real cuyo cuadrado sea -4. De otra forma:
, pues no existe ningún número real cuyo cuadrado sea -4. De otra forma:
Si consideramos la ecuación polinomial:
![]() ;
;
debido a que no existe número real x alguno que la satisfaga, consideraremos, para resolver este tipo de ecuaciones, el cuerpo de los números complejos y lo denotaremos C.
Definiremos un número complejo z como una expresión de la forma (x,y) donde x e
y son números reales.
A
la expresión:
z
= (x,y)
la
llamaremos forma cartesiana del complejo z,
donde:
·
x: parte
o componente real de z, (Re(z)).
· y:
parte
o componente imaginaria
de z,
(Im(z)).
Así pues definiremos el conjunto de los números complejos como:
C = {(x,y) / x,y Î R}
·
Casos particulares:
Si
x = 0 ®
al número complejo z= (0,y) lo llamaremos imaginario
puro.
Al
conjunto de los números IMAGINARIOS PUROS,
se le denota con iR.
Si
y = 0
®
al
número complejo z= (x,0) lo
llamaremos complejo
real.
Por
tanto R
·
Estructura
del conjunto de los Números Complejos:
(para
obtener la información, pulsar aquí)
· Representación:
La notación z = (x,y) nos hace pensar en un punto; en efecto, si consideramos el plano euclídeo y en él un sistema de referencia ortonormal, a todo número complejo z le podemos hacer corresponder un punto P llamado AFIJO de z y viceversa

A
este plano lo llamaremos plano complejo o diagrama
de Argand y a los ejes: al horizontal: eje real y al
vertical: eje
imaginario.
Gracias a esto, podemos “identificar”, el conjuntos de los números complejos, C, con el plano euclídeo R2.
·
Valor
absoluto o módulo de un número complejo:
Dado un complejo z =(x,y) , su módulo es el número real positivo:
|z|
=![]() .
.
El
módulo de un número complejo, representa geométricamente la distancia del
afijo de este número complejo, al origen de coordenadas.
·
Argumento de un número complejo:
· Opuesto
de un número complejo:
Dado
el número complejo z=(x,y) se define su opuesto como
|
|
Geométricamente:
supongamos para fijar ideas que x, y son positivos.
Observamos
que sus afijos son simétricos respecto al origen, y que sus argumentos
difieren en un múltiplo impar de p radianes:
Si el argumento de z es q y el de su opuesto j:
![]()
· Complejo conjugado:
El
conjugado de un número complejo z = (x,y), es
(x,-y), y se denota por![]() , o z*.
, o z*.
|
|
al eje x , y que sus argumentos son opuestos.
Si el argumento de z es q y el de su opuesto j:
![]()
Evidentemente,
podemos observar en el dibujo, que z y![]() , tienen el mismo módulo.
, tienen el mismo módulo.
Se define la exponencial compleja o imaginaria eiq, q Î R, i: unidad imaginaria, como:
![]()
Todo
número complejo se puede expresar en forma exponencial; sea z=(x,y);![]() .
.
![]()
![]() Fórmula
de Euler
Fórmula
de Euler
AVISO:
Sabemos
por trigonometría, que dado un valor de la tangente de un ángulo, podemos
encontrar, salvo vueltas de circunferencia, dos ángulos con la misma tangente
(los del Ier y IIIer cuadrante si la tangente es positiva,
y los del II y IV cuadrante si es negativa). Por eso, deberemos saber qué
argumento es el adecuado para el número complejo con el que estemos trabajando,
y eso vendrá dado por el cuadrante en el que se encuentre el afijo de dicho
número.
· Propiedades de la exponencial compleja:

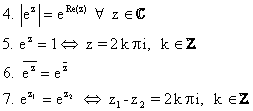
Notar
que la función exponencial compleja no es inyectiva.
![]()
Dem: Por inducción:
n=1
cierto
Supongo
cierto para n=k ![]()
Para k+1:
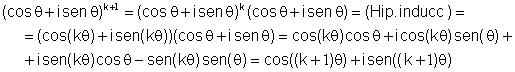
La aplicación de la fórmula de de Moivre en forma polar sería:
![]()
y en forma exponencial:
![]()
·
Formas de
expresión de un número complejo
FORMA BINÓMICA:
z = x + y i
donde x, y son reales; i representa la unidad imaginaria: con la propiedad de que
![]()
FORMA TRIGONOMETRICA:
![]()
FORMA
POLAR z
= mq
FORMA
EXPONENCIAL: z = meiq
Ejercicio:
Utilizando la fórmula de de Moivre,
calcular:
![]() en forma binómica.
en forma binómica.

·
Fundamentos
de los complejos
Sean
z1 = (a,b), z2 = (c,d) dos números complejos.
·
IGUALDAD:
z1
= z2
|
F. Cartesiana z1 = (a,b), z2 = (c,d) |
a,b)
= (c,d)
a = c; b = d |
|
F. Binómica z1 = a + bi, z2= c + di |
a+b i = c+d i
a=c;b=d |
|
F.
Polar
z1 = mJ |
|
|
F.Trigonométrica z1 = m(cos(J) + isen(J)) z1
= n(cos(j)
+ isen(j))
|
|
|
F.
Exponencial z1 = meiJ |
|
Notar
que, geométricamente: dos números complejos son iguales si sus afijos
coinciden.
·
SUMA:
z1 + z2
RESTA
z1
- z2
|
F. Cartesiana z1 = (a,b), z2 = (c,d) |
(a,b) ± (c,d) = (a ± c, b ± d) |
|
F. Binómica z1 = a + bi, z2= c + di |
(a+bi)
±
(c+di) = (a ±
c)+(b ±
d)i |
· PRODUCTO: z1 * z2
|
F. Cartesiana z1 = (a,b), z2 = (c,d) |
(a,b)* (c,d) = (ac-d,ad+bc) |
|
F. Binómica z1 = a + bi, z2= c + di |
(a+bi)*(c+di)=(ac-bd)+(ad+bc)i |
|
F.
Polar
z1 = mJ |
mJ |
|
F.Trigonométrica z1 = m(cos(J) + isen(J)) z1
= n(cos(j)
+ isen(j))
|
m(cos(J) + isen(J)) * n(cos(j) + isen(j)) = m * n(cos(J + j) + isen(J +j)) |
|
F.
Exponencial z1 = meiJ |
(m
*
n)ei(J+j) |
· COCIENTE z1 / z2 z2 ¹ 0
|
F. Cartesiana z1 = (a,b), z2 = (c,d) |
|
|
F. Binómica z1 = a + bi, z2= c + di |
|
|
F.
Polar
z1 = mJ |
|
|
F.Trigonométrica z1 = m(cos(J) + isen(J)) z1
= n(cos(j)
+ isen(j))
|
|
|
F.
Exponencial z1 = meiJ |
|
Si z1, z2,...,zm son números complejos, son válidas las siguientes propiedades:
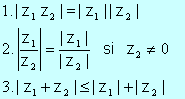
![]()
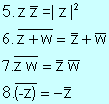


·
Raíces
de ecuaciones polinómicas
Llamaremos ecuación polinómica de grado n, con coeficientes complejos, a una ecuación de la forma:
![]()
A las soluciones de esta ecuación las llamaremos ceros o raíces.
Según el Teorema fundamental del Algebra: una ecuación de la forma anterior (con coeficientes complejos) tiene al menos una raíz compleja. O lo que es equivalente: n raíces complejas incluida la multiplicidad. Según esto, podré expresarla de la forma:
an
(z-z1)(z-z2)...(z-zn) =
0 zi : raíz
·
Caso particular:
Vamos a analizar una ecuación de la forma:
zn
- d = 0 donde z,d Î
C
Sea el número complejo d = a + bi y n un número natural no nulo. Se dice que el número complejo z es raíz n-ésima de d si se verifica que:
zn
= d (se escribe ![]() ).
).
En general, todas las raíces n-ésimas de un número complejo cualquiera se calculan expresando dicho número en forma trigonométrica, siguiendo la fórmula:
![]()
donde
k toma todos los valores entre 0 y n-1.
Así pues, todo número complejo tiene n raíces complejas distintas,
cuyos módulos son iguales a la raíz n-ésima del módulo del radicando, y
cuyos argumentos difieren en 2p
Dem:
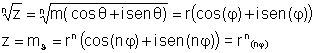
de donde, por la igualdad de dos números en forma polar:
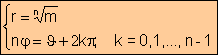
Como
un número complejo x + iy se puede considerar como una pareja ordenada de números
reales, podemos representar estos números por puntos en un plano xy, llamado el
plano complejo o diagrama de Argand. Así,
a cada número complejo corresponde uno y solamente un punto en el plano, salvo
un múltiplo entero de 2
en cuanto al ángulo o fase, y recíprocamente, a cada punto en el plano
corresponde uno y solamente un número complejo.
A
causa de esto, a menudo mencionaremos al número complejo z como al punto z, nos
referiremos a los ejes x e y como a los ejes real e imaginario respectivamente y
al plano complejo como al plano z.
· Distancia entre dos números complejos.
La
distancia entre dos puntos z1 = x1 +iy1
y z2 = x2 +iy2
en el plano complejo está
dada por:
![]()
·
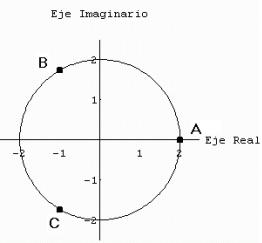
Representación de las raíces n-ésimas de un número complejo.
Sabemos
ya que todo número complejo tiene n raíces complejas distintas, cuyos módulos
son iguales a la raíz n-ésima del módulo del radicando, y cuyos argumentos
difieren en 2p
A
todo número complejo z le podemos hacer corresponder un punto P llamado afijo
de z cuyas coordenadas (x, y) en un sistema de referencia ortonormal en el
plano euclídeo son las componentes de z.
Llamando
R al afijo del número complejo z = mq
, los afijos de las n raíces están situados en la circunferencia de centro 0 y
radio ![]() y separados unos de otros por arcos que difieren en
2p
y separados unos de otros por arcos que difieren en
2p
En
el ejemplo siguiente los puntos A, B, C son los afijos de las tres raíces ![]()

·
Función exponencial:
Dado z = x + iy perteneciente a C se define la función exponencial compleja de la siguiente forma:
![]()
![]()
a).
Es periódica, de periodo 2pi
b).
Es holomorfa en todo C,
siendo su derivada ella misma.
·
Funciones trigonométricas/hiperbólicas:
|
Función |
Derivada |
|
|
-sen(z) |
|
|
cos(z) |
|
|
senh(z) |
|
|
cosh(z) |
·
Función Logaritmo:
Dado un número complejo z = mq , se define la función logaritmo compleja como:
![]() k Î
Z
k Î
Z
Log(z)=ln|z| + i (Arg(z) +2kp)
z ¹
0
donde
ln|z| es el logaritmo neperiano del número real |z|, ( y por lo tanto es la
función logaritmo real de variable real, ya conocida) Arg(z) Î
[0,2p[
es el argumento principal de z.
Si
el argumento del número complejo es menor que 2p
en valor absoluto, llamaremos al
logaritmo correspondiente valor
principal del logaritmo. Todos los demás valores del logaritmo se
obtienen sumando al valor principal múltiplos de 2p
i.
·
Potencias
de base y exponente complejo:
Se define la potencia de base z = mq y exponente t = a+ bi del siguiente modo:
![]()
1).
¿Por qué se creó el cuerpo de los números complejos?
2).
Define: a). número
complejo
b). parte real de un número complejo
c). parte imaginaria de un número complejo
d). imaginario puro
e). complejo real
f). Valor absoluto
g). argumento
h). opuesto
i). conjugado
3).
Enuncia la fórmula de Euler o de
la exponencial compleja
4).
Enuncia la fórmula de Moivre
5).
Representa un número complejo z en sus formas binómica, trigonométrica, polar
y exponencial.
6).
Halla el producto y el cociente de dos números complejos en forma binómica y
en forma polar. ¿Qué conclusión obtienes?
7). Completa las siguientes propiedades referentes al valor absoluto

![]()
8). Completa las siguientes propiedades referentes a la exponencial compleja

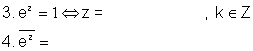
![]()
9).
Halla![]()
10). Resuelve: z5 = 1
11).
Las raices n-ésimas de un número complejo forman un …
1.Expresa los siguientes números complejos en forma binómica:
![]()
Solución:
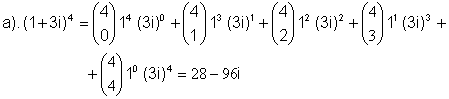
b). ![]()
![]()
2. Calcula el módulo de
los siguientes números complejos:
![]()
Solución:
![]()

![]()
3. Calcular el módulo y el argumento principal de los siguientes números complejos:
![]()
Solución:
![]()
![]()
![]()
![]()
![]()
![]()
4. Si x pertenece al conjunto de los números reales, probar que:
![]()
Solución:
Sabemos que, por la fórmula de la exponencial compleja o de Euler:
![]()
Si sumamos ambas expresiones:
![]()
Si las restamos:
![]()