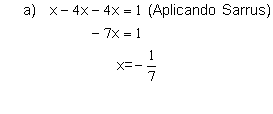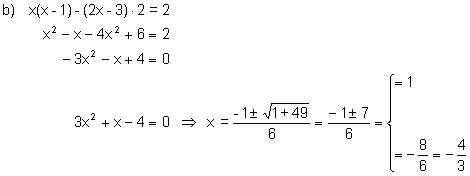DETERMINANTES
· Determinante de matrices elementales
· Fórmula de expansión de Laplace
· Estudio del rango de una matriz por determinantes
|
Temas relacionados: |
Las
matrices nacieron más de cien años después que los determinantes, de hecho
fue Sylvester quien llamó al término matriz la “madre de los
determinantes”. La mayor parte de los historiadores destacan a Leibniz y a
Newton como origen de la teoría de los determinantes, pero hay quienes creen
que fue Seki Kowa.

Takakazu Seki nació en una
familia de guerreros samurais, pero fue adoptado pronto por una familia noble.
Niño prodigio en matemáticas y autodidacta,
fue guiado en sus estudios por un criado de la casa. Se le conocía como “el
sabio aritmético”, término que fue tallado posteriormente en su piedra
sepulcral. En 1674 publicó “Hatsubi Sampo”, libro en el cuál solucionó 15
problemas que habían sido propuestos cuatro años antes. Estudió determinantes
en 1683, 10 años antes que Leibniz. Seki también descubrió los números de
Bernoulli antes de Jacob Bernoulli . También estudió
las ecuaciones que trataban raíces positivas y negativas sin tener ningún
concepto de números complejos.
En
1685, solucionó la ecuación cúbica
![]() usando el mismo método
que
Horner cientos de años más adelante. Descubrió también el llamado
método
de Newton-Raphson para solucionar ecuaciones. El secreto rodeó las escuelas en Japón así que es
difícil determinar las contribuciones hechas por Seki.
usando el mismo método
que
Horner cientos de años más adelante. Descubrió también el llamado
método
de Newton-Raphson para solucionar ecuaciones. El secreto rodeó las escuelas en Japón así que es
difícil determinar las contribuciones hechas por Seki.
 AUGUSTIN-LOUIS BARÓN DE CAUCHY
AUGUSTIN-LOUIS BARÓN DE CAUCHY
(1789-1857)
Matemático francés, uno de los especialistas más insignes de su
tiempo. Publicó numerosas investigaciones sobre teoría de funciones de
variable compleja, series, interpolación, ecuaciones diferenciales y cuestiones
de física, matemática y astronomía. Aparte de numerosas investigaciones,
publicó un Tratado de cálculo diferencial e integral y un Curso de análisis,
obras en las cuales se hallan sus principales ideas. Fue
profesor
de la Escuela Politécnica y del Colegio de Francia.
En 1812 escribió una memoria
que contenía la primera demostración del teorema
Det(ab)=Det(A) Det(B)
En 1840, Cauchy describió la
ecuación característica de la matriz A como el polionomio ![]() .
.

CHARLES
LUTWIDGE DODGSON
(1832-1898)
Charles Lutwidge Dodgson es
mejor conocido por el seudónimo "Lewis Carroll". Aunque él era matemático,
fue conocido como el autor de las aventuras de “ Alicia en el país de las
maravillas” (1865). Para sus trabajos matemáticos usó su propio nombre pero
para los libros de cuentos inventó el nombre "Lewis Carroll"
traduciendo sus primeros dos nombres "Charles Lutwidge" en latín como
"Carolus Lodovicus", y después inglesando e invirtiendo su orden.
En 1867
escribió “An Elementary Theory of Determinants”, donde da condiciones para
que los sistemas de ecuaciones tengan soluciones no triviales. Dichas
condiciones se expresan en términos de los determinantes de los menores de las
matrices de coeficientes.
El determinante no es más que una aplicaeción que va desde el conjunto de las matrices cuadradas de orden n al conjunto de los números reales

Ejemplo: cálculo del determinante de una matriz de orden 2:
![]()
Propiedades:
|
1). El
determinante cambia de signo cada vez que se intercambian dos filas. |
2).
El determinante es una función lineal (*) de la fila i-ésima. |
3).
Det(
|
(*)Función lineal
f: E--->F es lineal si ![]()
f(x+y)=f(x)+f(y)
f(kx)=kf(x)
Ejemplo: es una función lineal de la primera fila:


Nota: Esto no quiere decir que
Det(A+B)=Det(A)+Det(B) Esto
es falso
Ejemplo: cálculo del determinante de una matriz de orden 3:
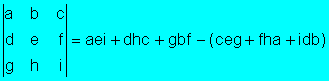
· Propiedades
Sea una matriz Anxn kÎR
1). Si A tiene dos filas
(o columnas) iguales, su determinante es nulo.
2). Si A tiene una fila (o columna) de ceros, su
determinante es nulo.
3). Las operaciones
elementales de tipo 3 no varían el valor del determinante.
4). Si en A, una fila
(o columna) es combinación lineal (*) de las demás, su determinante es nulo.
5). El determinante
de una matriz diagonal es el producto de los elementos de la diagonal
principal. Es decir: 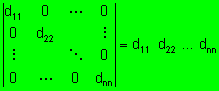
6). El determinante de una matriz triangular
superior es el producto de los
elementos de la diagonal principal. Es decir: 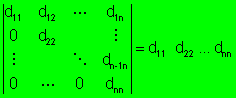
Idem triangular
inferior.
7).
det(KA) = Kn
det(A)
8). El determinante
de una matriz cuadrada es único.
Nota: Decir que una fila,
por ejemplo F1
, es combinación lineal de las demás significa que existen escalares (números
reales)![]()
·
Teorema
de Binet-Cauchy
Anxn, Bnxn ® Det(AB) = Det(A) Det(B)
·
Teorema
Anxn
invertible «
·
Determinante
de matrices elementales
Si E matriz elemental de tipo 1, (resultante de
realizar sobre la matriz identidad una permutación de filas)
Det(E)=-1
Ejemplo:
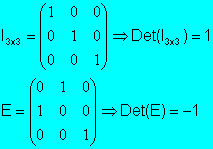
Si E matriz elemental de tipo 2, que resulta de
multiplicar una fila en la matriz identidad por un escalar k
Det(E)=k
Ejemplo:
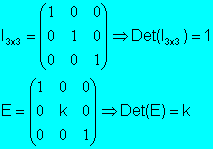
Si E matriz elemental de tipo 3, que resulta de
multiplicar en la matriz identidad, una fila por un escalar k y sumar el
resultado a otra fila, entonces el determinante no varía
Det(E)=1
Ejemplo:
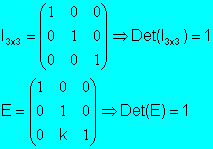
Si E es una matriz
elemental de tipo: 1, 2 ó 3, entonces
![]()
·
E, tipo 1
E es simétrica, por tanto E
= ET. Además: E-1
= E = ET
Si aplicamos determinantes:
![]()
·
E tipo 2,
E es diagonal por tanto E = ET
Si aplicamos determinantes:
![]() y
y
![]()
· E tipo 3 El valor del determinante con operaciones de tipo 3 no varía,
![]()
ET
es del mismo tipo que E, con lo
cual Det(ET)=1 y
Det(E-1)=1
·
Proposición
Si A es una matriz de tamaño mxn, entonces
![]()
·
Regla
de Cramer:
Consideremos el sistema Ax=b, donde A es invertible. Entonces la solución viene dada:

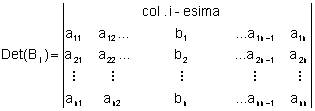
Sea una matriz Anxn
, llamaremos MENOR COMPLEMENTARIO A(i,j) al determinante de la matriz de tamaño
(n-1)x (n-1) que resulta de suprimir la fila i y la columna j; lo denotaremos Mij
(A).
·
Cofactor
Se define COFACTOR (i,j) de una matriz Anxn como el menor correspondiente afectado de signo, es decir:
![]()
Notar que al término (-1)i+j
se le llama signatura.
·
Fórmula
de expansión de Laplace
· Desarrollo por la fila i-ésima, columna j-ésima
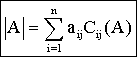
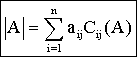
·
Matriz
adjunta

Nota: algunos autores definen la matriz adjunta de A como la matriz traspuesta de la definida anteriormente.
·
Matriz
de Vandermonde
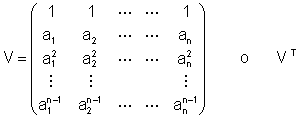
El valor del determinante de una matriz de Vandermonde (llamado determinante de Vandermonde) viene dado por la siguiente fórmula.
![]()
·
Estudio
del rango de una matriz por determinantes
Si bien en el tema correspondiente de sistemas de ecuaciones lineales definíamos el rango de una matriz A como el número de unos principales de su forma escalonada (o escalonada reducida), vamos a dar una definición paralela.
Definiremos el rango de una matriz de tamaño mxn como el orden del mayor menor no nulo.
Ejemplo:
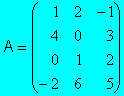
Estudiamos los menores de orden 3, hasta que alguno
de distinto de cero
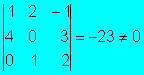 , luego el rango es tres.
, luego el rango es tres.
Supongamos que los n
pares de datos (x1,y1), (x2,y2),...,(xn,yn)
cumplen que los valores de xi
son todos distintos. Entonces
existe un único polinomio de grado menor o igual que n-1, tal que p(xi)=yi,
para i=1,2,...,n.
Este sistema tiene como matriz de coeficiente la matriz de Vandermonde.
1. Calcula el valor de los siguientes determinantes aplicando operaciones elementales y las propiedades relacionadas con ellas.

Solución:
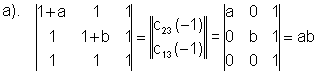

Aplicando la propiedad de que el determinante de una matriz triangular es el producto de los elementos de la diagonal principal, queda:
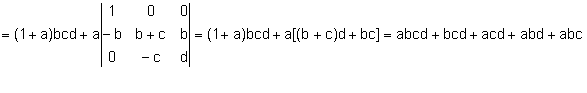

2). Resuelve las siguientes ecuaciones:
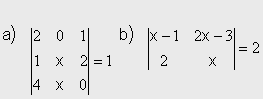
Solución: