 ARTHUR
CAYLEY (1821-1895)
ARTHUR
CAYLEY (1821-1895)MATRICES
· Descomposición L U de una matriz
|
Temas relacionados: |
 ARTHUR
CAYLEY (1821-1895)
ARTHUR
CAYLEY (1821-1895)
Nació en Richmond
(Inglaterra) en 1821. Se atribuyen a Cayley las reglas que indican cómo
se suman y multiplican las matrices. Compaginó durante varios años sus
estudios de matemáticas y el ejercicio de la abogacía hasta 1863 que ocupó la
cátedra Sadleriana, pudiendo, desde entonces dedicar todo su tiempo a las matemáticas.
Cayler se considera el tercer
escritor más prolífico de matemáticas, siendo superado sólo por Euler y
Cauchy. Hizo importantes contribuciones a la geometría analítica, la teoría
de los determinantes, la teoría de las curvas y superficies, …
Poseía una memoria asombrosa además
de un temperamento ecuánime, cualidades por las que fue llamado “el matemático
de los matemáticos”. Fue gran aficionado de la lectura de novelas, las cuales
leía mientras viajaba, mientras esperaba a una reunión, ….
Las matrices surgieron con Cayley al trabajar con transformaciones lineales del tipo:
![]()
Denotaremos una matriz como Am´n o A Î Mm´n(K) donde K es un cuerpo, generalmente K=R o K=C.
Dos matrices A, B son iguales si tienen el mismo tamaño y los elementos que ocupan los mismos lugares coinciden.
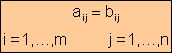
· Matriz cuadrada
Si el número
de filas es igual al de columnas; su tamaño es nxn (orden n)
Caso particular: las matrices diagonales que son aquellas que tienen nulos los elementos situados fuera de la diagonal principal.
![]()
· Matriz columna
Matriz de tamaño nx1
· Matriz fila
Matriz de tamaño 1xn
·
Matriz
identidad
Es una matriz cuadrada que tiene los elementos de la diagonal principal iguales a la unidad y el resto de elementos son nulos.
![]()
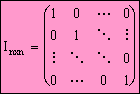
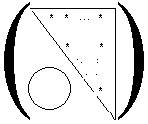
·
Matriz
triangular superior (t.s.)
Es aquella con elementos nulos por debajo de la diagonal principal
![]()
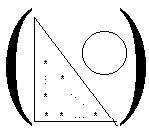
·
Matriz
triangular inferior (t.i.
Es aquella con elementos nulos por encima de la diagonal principal
![]()
|
1). El producto de matrices t.s. (t.i.) es t.s. (t.i.) 2). La inversa (*) de una matriz triangular (sea t.s. ó t. i.) en caso de existir, es también triangular (sea t.s. ó t. i.). |
(*)Se verá más tarde
·
Matriz
transpuesta
Dada
Am´n
llamaremos
matriz transpuesta de A (o traspuesta) a la matriz que resulta de cambiar las
filas por las columnas, la representaremos por
AT.
·
Matriz simétrica
Si cumple AT = A
![]()
Nota: necesariamente debe ser
cuadrada.
·
Matriz antisimétrica
Si cumple -AT = A
![]()
Nota: necesariamente debe ser
cuadrada y los elementos de la diagonal principal deberán ser nulos.
·
Suma de
matrices
Para sumar dos matrices deberemos tener en cuenta que sean del mismo tamaño.
Propiedades:
|
Conmutativa: Asociativa: Elemento neutro (es único): Elemento simétrico (es único): |
A + B = B + A (A+B) + C = A + (B+C) La matriz nula O para una matriz A es -A / A + (-A) =O |
· Producto por escalar
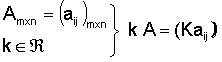
Propiedades:
Sean Am´n, Bm´n,
Cm´n, p,q
Î
R compatibles para las operaciones a
realizar
|
Distributiva
del producto por escalar respecto de la suma: Distributiva del
producto por escalar respecto de la suma de escalares: Asociativa del producto por un escalar: Existencia de elemento neutro para la multiplicación por escalar: |
P (A+B) = pA+pB
(p+q) A = pA+qA (pq) A=p (qA)
1 A=A |
· Producto de matrices
Para multiplicar dos matrices A y B el número de columnas de A deberá ser igual al número de filas de B.
|
1.
Asociativa (A B) C=A (B C) |
|
2.
Distributiva del producto respecto a la suma de matrices por la izquierda A (B+C)=A B+A C |
|
3.
Distributiva del producto respecto a la suma de matrices por la derecha (B+C) D=B D +C D |
|
4. Asociativa del producto por escalar y el producto de matrices k (A
B)= (k A) B=A (k B) |
En general, el producto de matrices no es conmutativo.
Dos matrices A y B conmutan![]()
![]()
![]() Aplicando la distributiva
Aplicando la distributiva
![]()
![]()
![]()
![]()
![]()
Teorema
![]()
![]()
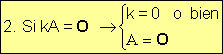
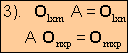
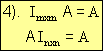
Teorema:
![]()
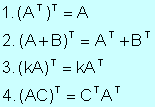
Una matriz cuadrada de tamaño nxn se dice que es una matriz elemental de tipo I, si es el resultado de aplicar sobre la Identidad una operación elemental de tipo 1.
Idem tipos 2, 3. Representaremos estas matrices con la letra E.
Realicemos una operación
elemental sobre una matriz A y a la matriz resultante llamémosla R.
Seguidamente realizamos la misma operación elemental sobre la identidad, y el
resultado es una matriz elemental llamada E. El resultado de premultiplicar la
matriz A por la matriz elemental E es la matriz R.
EJEMPLO:
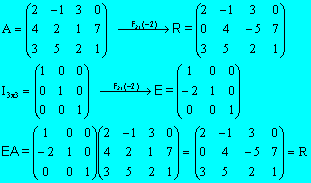
![]()
Sea
Anxn, se dice que Bnxn es una inversa de A si
AB=BA
= Inxn
·
Una
matriz con una fila de ceros no tiene inversa
·
Si
una matriz tiene inversa, ésta es única
1). Si A es invertible, entonces A-1 también es invertible y
(A-1)-1 = A
2). Si A y B son invertibles, el producto también
lo es:
(AB)-1 = B-1A-1
En cambio, si una de las dos no es invertible, el
producto tampoco
3). Si A es invertible y k
¹
4). Si A es invertible, también lo es AT y (AT)-1 = (A-1)T
5). Si Anxn y Bnxn
/ AB = Inxn
|
Si A es invertible
Este criterio suele aplicarse para los S.E.L. completos: Si
|
|
Si por el contrario:
Este criterio suele aplicarse en los sistemas de ecuaciones lineales homogéneos
|
· Aplicación
Como hemos visto anteriormente, si realizamos n operaciones elementales sobre una matriz A, la resultante será
![]()
Vamos a llamar T a la matriz transformación que resulta del producto de las n matrices elementales.
![]()
En forma de algoritmo:
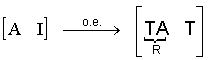
Si R fuese la matriz identidad, la matriz T sería la inversa de A.
·
Inversas de
las matrices elementales
Todas las Ei son invertibles y su inversa es del mismo tipo, por tanto la matriz T, definida anteriormente, también será invertible.
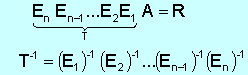
·
Inversas de
las matrices triangulares
![]()
![]()
·
Rango
Llamaremos rango de una
matriz A al número de unos
principales de su forma escalonada (f.e.) ó su forma escalonada
reducida (f.e.r.).
Teorema
Si Anxn Equivalen:
1). A invertible
2). rg(A)=n
3). A se puede transformar en In mediante operaciones elementales
4). A es producto de matrices elementales.
5). ![]()
Corolario
1). A es invertible
2). La f. e. de A es
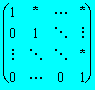
3). La f.e.r. de A es
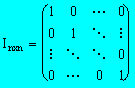
4). El sistema homogéneo AX=O sólo admite la
solución trivial
5). El sistema AX=b es C.D
· Descomposición L U de una matriz
Toda matriz Amxn
se puede expresar como producto de
dos matrices L y U, donde:
·
U es una matriz triangular superior, de tamaño m x
n y resultante de aplicar sobre la matriz A sólo
operaciones del tipo 3.
·
L es una matriz triangular inferior, de orden m,
cuyos elementos en la diagonal principal son iguales a 1, y cuyos elementos por
debajo de la diagonal principal se obtienen a partir de las operaciones
elementales del tipo 3 realizadas sobre la matriz A para obtener U. Por ejemplo,
si hemos realizado la operación
F21(-3), la operación inversa sería F21(3), por tanto el elemento (2,1) de la matriz L sería igual a 3.
· Aplicación
Queremos resolver un sistema
AX = b
A
= LU Þ
aplico la propiedad asociativa:
L(UX) = b
Llamo
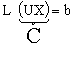
·
El
sistema UX=C es triangular superior y lo resolveremos fácilmente por sustitución
regresiva.
·
El
sistema LC=b es triangular inferior y lo resolveremos fácilmente por sustitución
progresiva.
1) Calcula T para que T·A=R, siendo R la forma escalonada reducida de A.
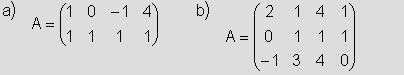
Solución:
a).
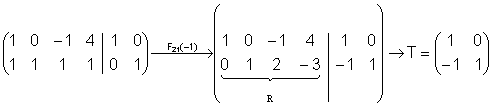
b).
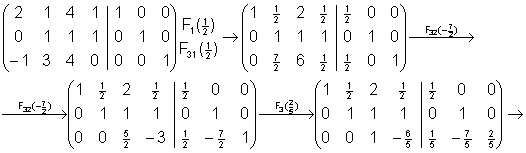
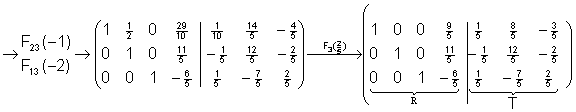
2) Halla la descomposición LU de la siguiente matriz:
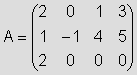
Solución:
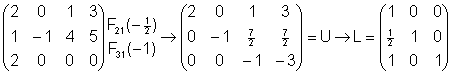
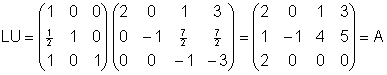
3) Calcula la matriz inversa, si existe de las siguientes matrices:
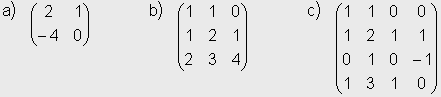
Solución:
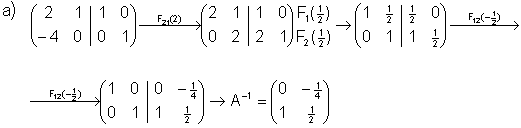
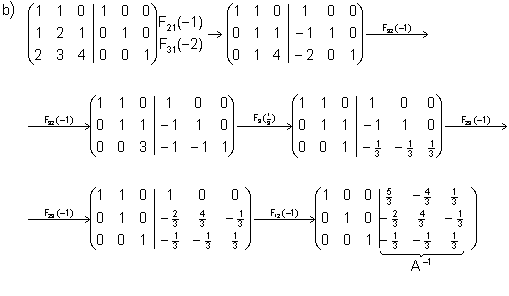
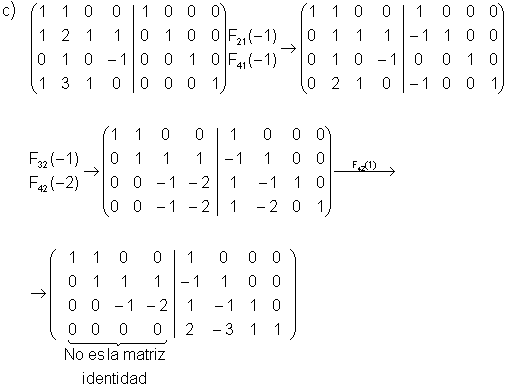
En este caso, la matriz A no es invertible.