·  Función logarítmica

·  Introducción

En 1544 Michael Stiefel (1487-1567), en su obra Aritmética Integra, puso de manifiesto que la suma en la serie aritmética 

se correspondía con la multiplicación en la serie geométrica 

 Por ejemplo, si queremos multiplicar 8 por 128, bastará sumar los números correspondientes en la serie aritmética (el 3 y el 7) y tomar el término correspondiente a su suma (10) en la serie geométrica, es decir 1024.

     Inspirándose probablemente en esta obra de Stiefel, el escocés Sir John Napier (1550-1617) publicó Mirifici Logarithmorum Canonis Descriptio, en el que por primera vez aparece por primera vez la denominación “logaritmo” con el objeto de reducir la multiplicación a una operación mucho más sencilla como la suma.

Esta gran ventaja práctica fue puesta de manifiesto por Kepler (1571-1630) que empleó las tablas de Napier en los enormes cálculos que le llevaron al descubrimiento de la ley del movimiento planetario.

         En 1615 Henry Briggs (1561-1630) construyó una tabla de logaritmos de base 10 que publicó en 1624 en Aritmetica Logatithmica. A estos logaritmos de base 10 se les conoce como logaritmos decimales, vulgares o de Briggs.

         En 1668 Mercator (1620-1687) publicó una nota en la que estudiaba los logaritmos que tienen por base el número e, a los que llamó logaritmos naturales; actualmente se les conoce también como logaritmos neperianos en memoria de Napier  o hiperbólicos.

 ·  Definición:

     Logaritmo en base a (a > 0, a ¹ 1) de un número x es el exponente al que tenemos que elevar la base para que resulte el número x.

     Deberemos recordar que ni los números negativos ni el cero tienen logaritmos. 

· Función logarítmica

Dado el real positivo a, distinto de la unidad, diremos que log_a(x) es el logaritmo en base a de x; la función logarítmica de base a es una aplicación de R⁺ en R , dada por:

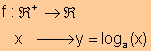
        De la definición podemos deducir:

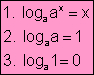
Ejemplo:

Halla y=log₃81 

3^y = 81

3^y = 3⁴ Û y = 4

  Nota:

La función logarítmica es la función inversa de la función exponencial de la misma base, puesto que log_ax = y Û a^y = x.  

  Las gráficas de dichas funciones son simétricas respecto a la bisectriz del primer y tercer cuadrante; veamos un ejemplo.

Ejemplo:

Representemos las funciones y = 3^x, y = log₃x

  Nota:  

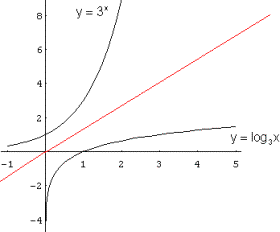
Si se toma el número 10 como base (a=10), se llama logaritmo decimal, y suele denotarse log x.  

Si la base a = e » 2.71 se llama logaritmo neperiano y se denota ln(x);  

Ejemplo:

La representación de la función y=ln(x) en el  intervalo ]0,6[ es:

  ·                    Propiedades algebraicas de la función logaritmo

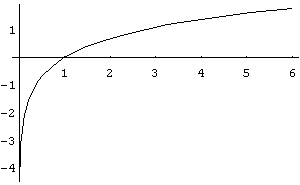
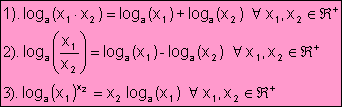
Además:

En cuanto a la gráfica de la función logaritmo:

  ·              Cambio de base en los logaritmos

      Como consecuencia de las propiedades de los logaritmos, éstos son útiles para simplificar cálculos complicados, sustituyendo las potencias por multiplicaciones, las multiplicaciones por sumas, las raíces por divisiones, las divisiones por restas; aunque en la actualidad los ordenadores sean capaces de hacer dichos cálculos con mucha mayor rapidez y precisión.  

  ·              Ecuaciones logarítmicas

Son aquellas ecuaciones en las que la incógnita figura bajo el signo de la función logaritmo.  

Ejemplo: comprobar

Resolver la siguiente ecuación logarítmica: log(2x + 6) =2  

10² = 2x + 6 Û 100 = 2x + 6

                     100 - 6 = 2x

                             94 = 2x

  ·              Sistemas de ecuaciones exponenciales y logarítmicas

Para resolver sistemas de ecuaciones donde intervengan ecuaciones exponenciales y/o logarítmicas, transformaremos en primer lugar el sistema en otro en el que intervengan ecuaciones algebraicas, para lo cual se utilizará tanto la definición como las propiedades conocidas tanto para logaritmos como para exponenciales.  

Ejemplo:

Resolver el siguiente sistema:

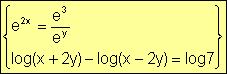
· Operando en la primera ecuación queda:

e^2xe^y = e³ Û e^2x+y = e³ Û

· Operando en la segunda ecuación queda:

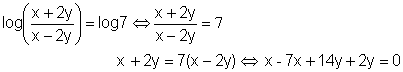
Con lo cual el sistema queda transformado como sigue:

con solución