·  Introducción

    ·  Sistema de ecuaciones lineales (S.E.L.)

    ·  Operaciones elementales

    ·  Forma escalonada de una matriz

    ·  Forma escalonada reducida de una matriz (f.e.r.)

    · Sistemas equivalentes

    · Algoritmo de Gauss

    · Clasificación de los S.E.L.

    · Teorema de Rouché-Frobenius

    · Sistemas Homogéneos

    · Ejercicios resueltos

·  Introducción

KARL-FRIEDRICH GAUSS(1777-1855)

Nació en Gotinga (Alemania), el 30 de abril de 1777. Su madre era una mujer inteligente pero poco instruida y su padre, llamado Gerhard, fue calificado por Karl como “digno de estima”, pero también como “dominante, rudo y poco refinado”.

 Su madre había sido sirvienta antes de convertirse en la segunda esposa de su padre, que vivía pobremente ejerciciendo diversos oficios: jardinero, jornalero, contramaestre para el mantenimiento de las canalizaciones, etc. De niño, Karl debía ser respetuoso y obediente con un padre que no veía la utilidad de instruir a su hijo. Por el contrario, su madre esperaba mucho de su “maravilloso” Karl, y aunque su matrimonio fue bastante desgraciado, se consagró enteramente a la carrera de su hijo. Gauss testimonió mucho afecto y gratitud durante toda su vida a su madre, que murió a los 97 años, habiendo pasado los últimos 22 años de su vida en la casa de Karl.

 Sin ayuda de ningún tipo, Gauss aprendió a “calcular antes de hablar”. A los tres años corrigió un error en la paga de los obreros de su padre, y por sí sólo estudió y profundizó la aritmética. A los 8 años mostró su genio precoz con ocasión de un problema propuesto por su profesor de la escuela elemental para ocupar a sus alumnos: encontrar la suma de los 100 primeros números naturales.

 Gauss formuló el método de los mínimos cuadrados, descubrió la ley de reciprocidad cuadrática, la hipótesis del teorema de los números primos y encontró resultados compatibles con una geometría no euclídea. A los 19 años obtiene la construcción del polígono regular de 17 lados con sólo la regla y el compás.

 Gauss, a quien le gustaban el rigor y la perfección, publicaba muy poco y muy tarde. Su tesis de doctorado, a los 22 años, contiene una demostración de que toda ecuación polinómica, p(x)=0, posee al menos una raíz, cualquiera que sea la naturaleza real o imaginaria de los coeficientes de la ecuación: (Teorema Fundamental del Álgebra). 

·   Sistema de ecuaciones lineales (S.E.L.)

Un sistema lineal de m ecuaciones y n incógnitas, tiene la forma

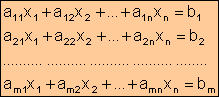
donde:

                                    coeficientes del sistema

                                                 términos independientes

                                               incógnitas ó variables del sistema

Si algún b_i  es no nulo, el sistema de ecuaciones  se denomina completo.

Una forma análoga de representación es:

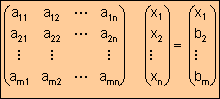
                                            A =Matriz de 

                              coeficientes                                                                               

                                                          x=Vector de 

                                                           incógnitas

                                                                      b=Vector de términos

                                                                      independientes

Los S.E.L. también quedan perfectamente definidos conociendo la matriz ampliada del sistema.

·   Operaciones elementales 

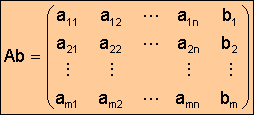
1). Intercambio de ecuaciones ( ó filas). Denotaremos F_ij

2). Multiplicación de una ecuación  (fila) por un número no nulo. Denotaremos F_i (k)

3). Sumar a una ecuación (fila) otra multiplicada por un número. Denotaremos F_ij (k)

·   Forma escalonada de una matriz

Diremos que una matriz está en forma escalonada si:

 1). El primer elemento no nulo (por la izquierda) de cada fila es un 1, que llamaremos UNO PRINCIPAL.

 2). Cada UNO PRINCIPAL está a la derecha de los unos principales de las filas anteriores.

 3). Las filas nulas, si existen, están en la parte inferior de la matriz.  

Ejemplo:

Las siguientes matrices se hallan en forma escalonada. Los * representan números  cualesquiera.

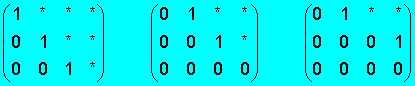
·   Forma escalonada reducida de una matriz (f.e.r.)

Una matriz se dice que está en forma escalonada reducida si es escalonada y además cada columna que tiene un uno principal, tiene nulos los demás elementos; pero las columnas que no tienen unos principales sí pueden tener elementos no nulos. 

Ejemplo:

Las siguientes matrices se hallan en forma escalonada reducida.

·   Sistemas equivalentes 

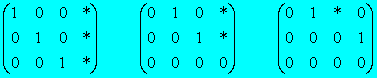
Diremos que dos S.E.L. son equivalentes si tienen el mismo conjunto de soluciones.

·    Solución de un S.E.L. 

Llamaremos  solución del sistema a una n-tupla que satisfaga cada una de las m ecuaciones.

     Se llama n-tupla a un conjunto ordenado de n números reales t₁, t₂,..., t_n

· Algoritmo de Gauss 

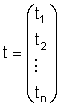
Es un método para resolver de forma sistemática, sistemas de ecuaciones lineales transformándolos en sistemas equivalentes más sencillos. 

Los sistemas más fáciles de resolver son:

 Diagonales:

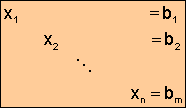
Triangulares :

 La matriz ampliada es escalonada

·        Superiores:

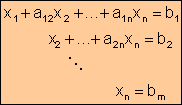
Estos sistemas se resuelven por sustitución regresiva. 

·        Inferiores:

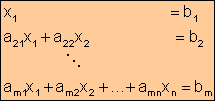
 Estos sistemas se resuelven por sustitución progresiva.

·   Algoritmo para hallar una forma escalonada

1) Elegir la fila pivote:

    Aquella que tenga un elemento no nulo más hacia la izquierda.

        1.1. Si no es la primera fila, permutar.  (Operación elemental tipo 1)                                  O.E.I

        1.2. Si el elemento es un 1: es ya el PIVOTE

        1.3. Si no, dividir la fila por dicho elemento. (Operación elemental tipo 2)                        O.E.II

2) Anular todos los elementos situados bajo el pivote. (Operación elemental tipo 3).                                                                                                                                                       O.E.III

3) Repetir el proceso.

·   Algoritmo para hallar una forma escalonada reducida

Además de los tres pasos anteriores:

4) Anular todos los elementos situados por encima del pivote.                                              O.E.III    

· Clasificación de los S.E.L.

· Teorema de Rouché-Frobenius 

Un S.E.L. es:  

 · Sistemas Homogéneos 

Son sistemas de la forma:

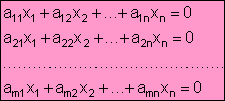
         Siempre son COMPATIBLES. Admiten siempre como solución la trivial 

x₁ = x₂ = ... = x_n = 0   

        Pudiendo admitir (ó no) otras soluciones. Si tiene más incógnitas que ecuaciones entonces tiene soluciones no triviales.

 Si la matriz escalonada reducida de un sistema homogéneo de n variables tiene r unos principales, entonces:

         La solución general tiene n-r parámetros.

La solución general de un S.E.L. completo viene dada por la suma de la solución general del homogéneo más una solución particular del completo.

= +

Así pues, si nos dan una solución particular del completo, bastará con hallar la solución general del homogéneo, pues al sumarlas tendremos la solución general del completo, sin necesidad de resolverlo, con el consiguiente ahorro de tiempo.

 · Ejercicios resueltos

Sol:

     Vamos a hallar la forma escalonada de la matriz ampliada del sistema mediante operaciones elementales para convertir este sistema en otro más sencillo de resolver.

     Como el primer elemento no nulo (por la izquierda) en la primera fila es ya un UNO, procedemos a anular los elementos situados por debajo, en la misma columna, mediante operaciones tipo 3: multiplicamos la primera por (-1) y sumamos a la tercera.

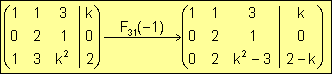
    Seguidamente, anulamos el elemento situado en la fila 3 y columna 2, también con una operación tipo 3.

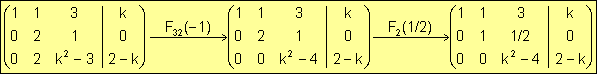
    El paso siguiente es conseguir un UNO en la posición (3,3), pero observamos que aparece un parámetro, por lo cual podremos dividir por dicha cantidad siempre y cuando sea no nula.

Caso 1.

Caso 2.

Sol:

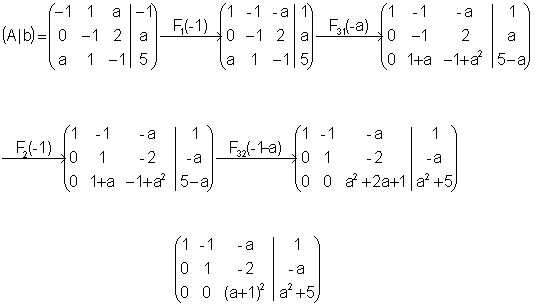
Caso 1.

Caso 2.