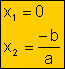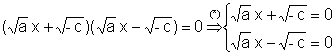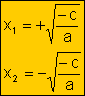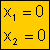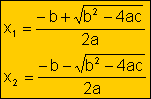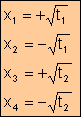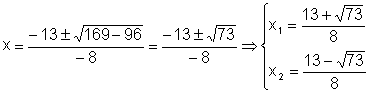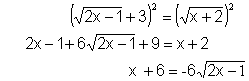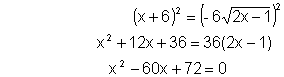ÁLGEBRA:
Del árabe (alchebr, reducción).
Rama de las matemáticas cuya finalidad fundamental es simplificar y
generalizar las cuestiones referentes a los números ó estudio de las
funciones numéricas. Como el estudio de una función lleva, en definitiva, al
planteamiento de una ecuación, se dice también que el álgebra es el estudio de las ecuaciones. La
simplificación nace del empleo, en el cálculo, de signos para indicar las
operaciones, y de letras, tanto para representar los valores conocidos o datos
(se suelen usar las primeras letras del alfabeto), como los valores
desconocidos que se buscan (últimas letras del alfabeto).
La forma más alta de generalización lleva a determinadas fórmulas, en las
que, reemplazando las letras por los datos, y efectuando las operaciones
convenientes, se llega a la determinación del valor desconocido.
Así por ejemplo, si se quiere saber el espacio recorrido por un cuerpo que se
cae, se utiliza la fórmula:
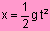
en
la que x representa la incógnita, g un valor fijo para cada lugar, la atracción
de la gravedad y t el tiempo que tarda el cuerpo en llegar al suelo.
Gauss demostró el Teorema
Fundamental de Álgebra, según el cual toda ecuación de
grado n-ésimo tiene n raíces.
Ya los antiguos egipcios (Ames) sabían
resolver ecuaciones de primer grado. Los griegos encontraron la solución de
segundo grado por métodos geométricos. Los hindúes (Bascara)
hallaron esa solución mediante el cálculo. La
escuela algebrista italiana: Scipione
del Ferro, Fontana
(alias Tartaglia, pues era tartamudo),
Cardano, Bombelli, … encontraron la solución de la ecuación de
tercer y cuarto grado.
Han contribuido al progreso del álgebra: Newton:
en el siglo XVII, Euler y
Lagrange,
en el siglo XVIII, Gauss,
Abel,
Galois
y Kronecker
en el siglo XIX. Descartes
y
Fermat
uniendo la geometría y el álgebra crearon la geometría
analítica.
Se llama igualdad al conjunto de
dos expresiones matemáticas unidas por el signo igual (=). Una igualdad puede
ser cierta o falsa. La expresión situada a la izquierda del igual se llama
primer miembro y la situada a la derecha se llama segundo miembro. Ecuación es
una igualdad en la que intervienen letras, y más formalmente:
| Sean f(x) y g(x) dos aplicaciones definidas entre
dos conjuntos A y B (que pueden ser iguales) y x un elemento de A. Se
llama ecuación
con una incógnita x, a la igualdad
f(x)=g(x). |
| De igual forma definiríamos ecuación con n incógnitas a la
igualdad
f(x1,x2,...,xn)
= g(x1,x2,...,xn)
siendo
f(x1,x2,...,xn) y g(x1,x2,...,xn)
dos aplicaciones definidas entre dos conjuntos An y B y (x1,x2,...,xn)
un elemento de An. |
Resolver una ecuación en un determinado conjunto, es
hallar los valores (x,y) en dicho conjunto, que sustituidos en lugar de las
incógnitas en las expresiones dadas dan lugar a igualdades numéricas.
|
Dos ecuaciones son equivalentes
si y sólo si el conjunto de soluciones de la primera coincide con el
conjunto de soluciones de la segunda.
Obtendremos una ecuación equivalente a la dada si se suma el
mismo número a los dos miembros y también si se multiplican los dos
miembros de la ecuación por un número real distinto de cero.
Si se elevan los dos miembros de una ecuación a la
misma potencia, resulta otra ecuación que tiene todas las raíces de la
primera o incluso alguna más.
En una ecuación se pueden transponer términos de un
miembro a otro, cambiándoles de signo. Las nuevas ecuaciones que así
resultan son equivalentes a la primera. |
Así
pues, las ecuaciones se pueden clasificar de dos formas distintas:
¨
si atendemos al número de incógnitas, diremos que
la ecuación tiene una, dos, tres o más incógnitas.
¨
según la naturaleza de las expresiones: en algebraicas
y trascendentes.
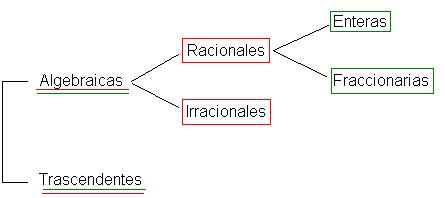
Diremos que una ecuación es algebraica si los dos miembros son expresiones formadas por las incógnitas
y números reales sometidos (un número finito de veces) a operaciones de suma,
resta, multiplicación, división, potenciación de exponente natural y radicación.
Las algebraicas se dividen a su vez en racionales (cuando no contienen
ninguna incógnita bajo signo radical) y en irracionales
en caso contrario. Las racionales, a su vez pueden ser enteras
(si no contienen ninguna incógnita como divisor) y fraccionarias
en caso contrario.
Diremos que una ecuación es trascendente si no es algebraica, (por ejemplo ln(x)=3x
).
·
Ecuaciones
de primer grado con una incógnita
Si tenemos una ecuación de
primer grado o lineal en forma típica o reducida
,
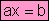con
coeficientes reales, podemos considerar los siguientes casos:
·
Ecuación de primer
grado con dos incógnitas
Una ecuación de primer grado con dos incógnitas en forma típica, normal o
reducida es:
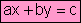
Esta
ecuación tiene infinitas soluciones.
·
Resolución
de sistemas de 2 ecuaciones de primer grado con dos incógnitas
Llamaremos sistema de 2 ecuaciones con 2 incógnitas
a un conjunto de 2 ecuaciones que se satisfacen simultáneamente por uno o más
conjuntos ordenados de valores de las 2 incógnitas que figuran en ellas.
Los sistemas que tienen solución, llamados
compatibles, se clasifican en
determinados (con solución única) e indeterminados (con infinitas soluciones).
La interpretación geométrica de un sistema de dos
ecuaciones con dos incógnitas compatible determinado es la de dos rectas en el
plano que se cortan en un punto. Si el sistema es compatible indeterminado
diremos que las rectas se superponen o son coincidentes
Si un sistema no tiene solución se dice que es
imposible (por tanto las ecuaciones son incompatibles). Geométricamente son dos
rectas paralelas.
Veremos a continuación mediante ejemplos, los métodos
empleados para hallar su solución general, (es decir, la intersección de las
soluciones generales de cada una de sus ecuaciones).
· Método de reducción
Ejemplo:
Sea
el sistema
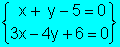
Vamos a hallar un sistema equivalente multiplicando
la primera ecuación por (-3)
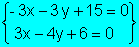
Ahora, la primera ecuación la sustituiré por la
suma de la primera y segunda, dando lugar a un sistema equivalente
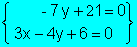
Seguidamente, despejaré en la primera ecuación el
valor de y y sustituiré en la
segunda ecuación.
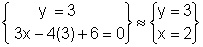
· Método de sustitución
Ejemplo:
Sea
el sistema
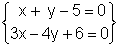
Vamos a hallar un sistema equivalente despejando x
en la primera ecuación y sustituyendo dicho valor en la segunda
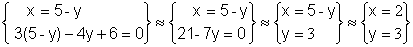
· Método gráfico
Ejemplo:
Sea
el sistema
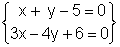
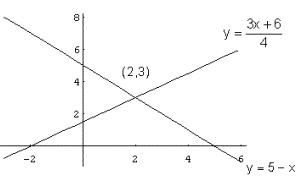
Si representamos gráficamente cada una de las
ecuaciones, obtenemos sendas rectas que se cortan en el punto (2,3).
·
Ecuación de segundo
grado o cuadrática
Una ecuación con una incógnita f(x)=g(x) se dice de 2º grado o cuadrática si
al menos una de las aplicaciones ( f, g) son
aplicaciones cuadráticas.
En
forma típica o reducida:
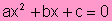
en
la que a, b, y c son números reales.
La
expresión y=ax2+bx+c
se llama
trinomio de segundo grado y su
representación gráfica es una parábola cuyo vértice tiene de abcisa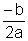
, con ramas hacia arriba si a>0 y hacia abajo si a<0 y eje de simetría
paralelo al de ordenadas por el vértice.
Clasificación:
¨ Incompletas: si b, c o ambos son nulos
¨ Completas: si todos los coeficientes (a,b,c)
son distintos de cero.
Una
ecuación de 2º grado tiene a lo sumo dos soluciones.
Resolución:
·
 
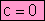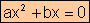
Saco factor común x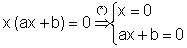 
Raíces:
|
(*)
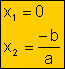
La ecuación producto f(x)·g(x) = 0
tiene por soluciones la unión de
los conjuntos de soluciones de las ecuaciones f(x)=0; g(x)=0.
·
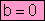
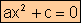a>0, c>0
Factorizo
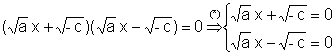
Raíces:
|
·
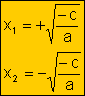
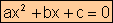
Multiplico por 4a
4a2x2 + 4abx + 4ac = 0
Sumo y resto b2 (4a2x2
+ 4abx + b2) - (b2 - 4ac) = 0
(2ax +b)2 - (b2 -4ac) = 0
Diferencia
de cuadrados
Teorema
ecuación producto
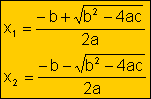
Según
el signo del discriminante de una ecuación (D) podemos saber cómo son sus raíces
Propiedades
de las raíces:
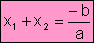
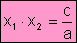
Si
conocemos las raíces de una ecuación de 2º grado, podemos obtenerla
mediante la siguiente fórmula
|
·
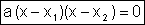
Ecuaciones
bicuadradas
Es la igualdad formal f(x)=g(x) que reducida adopta
la forma
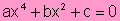
con
a ¹
0 y a,b,c números reales.
Para su resolución se toma el cambio
x2 = t, y sustituyendo resulta la ecuación de 2º grado
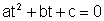
cuyas
raíces son t1
y t2; por tanto, las raíces de la bicuadrada
son:
·
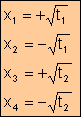
Ecuaciones
racionales
Es
la igualdad formal f(x) = g(x) que reducida adopta la forma
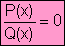
siendo
P(x) y Q(x) funciones polinómicas.
Teniendo
en cuenta la equivalencia por multiplicación,
·
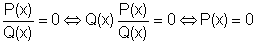
Ecuaciones irracionales cuadráticas
Es la igualdad formal f(x) = g(x) que contiene al
menos un radical cuadrático de un polinomio.
Para su resolución elevaremos al cuadrado los dos
miembros de la ecuación tantas veces como sea necesario hasta que desaparezcan
los radicales cuadráticos y cuando
sea posible factorizaremos.
Ejemplo:
Resolver
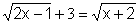
Elevamos
al cuadrado
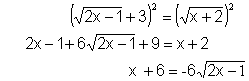
Elevamos
de nuevo al cuadrado
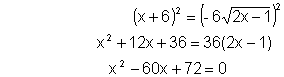
Y
ya tenemos una ecuación de 2º grado que sabemos resolver.
