
ESPACIOS VECTORIALES
· Definición de espacio vectorial (e.v.)
· Definición de subespacio vectorial (s.e.v.)
· Dependencia e independencia lineal
· Teorema de la base incompleta
· Suma e intersección de subespacios vectoriales
|
Temas relacionados: |

Nació
el 11 de febrero de 1839 en New Haven, USA
Murió
el 28 de abril de 1903 in New Haven, USA
Inició el estudio de análisis vectorial. Publicó su libro
“Vector Analysis” en 1881, y en
1902 su “Elementary Principles of
Satitistical Mechanics”.
Los estudiantes de matemáticas aplicadas encuentran el
curioso fenómeno de Gibbs en las series de Fourier.
Un vector en el espacio se considera como un segmento de recta dirigido o flecha. Gibbs dio las definiciones de igualdad, suma y multiplicación de vectores. Definió el producto escalar para los vectores i, j, y k de las siguiente forma:
![]()
Gibbs aplicó el producto escalar en un problema relativo a
fuerzas. Los vectores fueron
desarrollados por Gibbs y otros con el objeto de facilitar el análisis de los
fenómenos físicos.
·
Definición
de espacio vectorial (e.v.)
Se dice que E es un espacio
vectorial real si, dados tres elementos cualesquiera x,
y, z de E y dos números reales arbitrarios a, b, se cumplen las
propiedades:
A.1. x + y = y
+ x (conmutativa)
A.2. (x + y)+z
= x+ (y + z)
(asociativa)
A.3. x + 0 = 0
+ x = x
(el.
neutro)
A.4. x + (-x) = (-x)
+ x = 0
(el. opuesto)
A.5. a(x + y) = ax
+ ay
(distributiva)
A.6. (a + b)x
= ax + bx
(distributiva)
A.7. a(bx) = (ab)x
A.8. 1x = x
x,
y z : vectores (denotados en negrita) ; a,b: escalares
0: vector nulo
-x: vector opuesto de x
·
Propiedades
Si u,v
Î
E
y a,b
Î
R
Reglas
de productos nulos:
• 0v = 0
• a0 = 0
• Si av = 0, entonces a=0, ó v = 0
Reglas
de los signos:
•(-a)v =
a(-v) = -(av)
• (-a)(-v) = av
Reglas
de simplificación:
•Si au =
bu y u ¹
0, entonces a=b
•Si
au = av y a ¹ 0, entonces u
= v
·
Definición
de subespacio vectorial (s.e.v.)
Un subconjunto no vacío F de E
(espacio vectorial) es un subespacio
vectorial de E si él mismo es espacio vectorial.
F es un subespacio vectorial de
E, si y sólo si, se cumplen las siguientes condiciones: (ver ejercicio
1)
•F contiene al vector 0 de E.
•Si u y
v están en F, entonces u
+ v está en F.
• Si u
está en F y a es un escalar, entonces au
está en F.
Un subespacio vectorial
también se puede caractizar del siguiente modo:
•F contiene al vector 0 de E.
•Si u y v están en F, y a, b son dos escalares, entonces au + bv está en F.
Un vector x de un espacio vectorial E es combinación lineal de los vectores x1,x2,..., xp de E, si se puede expresar como
![]()
donde los escalares a1,a2,...,
ap reciben el nombre de coeficientes
de la combinación lineal.
Se llama ENVOLTURA LINEAL de los vectores x1,x2,..., xp de un espacio vectorial E, al conjunto de todas las combinaciones lineales de dichos vectores.
![]()
·
F es el menor subespacio
vectorial que contiene a los vectores x1,
x2,..., xp
Sea F un subespacio vectorial de E. Se dice que {x1,x2,..., xp} es un CONJUNTO
GENERADOR de F si F = Env
{x1,x2,..., xp}.
Si x es un vector de un espacio vectorial E que es combinación lineal
de los vectores x1,x2,...,
xp entonces:
Env {x1,x2,...,
xp} = Env {x1,x2,...,
xp,x}.
·
Dependencia
e independencia lineal
·
Definición
Un conjunto de vectores {x1,x2,..., xp} de un espacio vectorial E se dice que es linealmente independiente (o libre) y se escribe L. I., si la igualdad
![]()
sólo
se satisface cuando a1 = a2 = ... = ap
= 0.
En caso contrario, se dice que los vectores son linealmente dependientes (o ligados).
·
Propiedades
Sea {x1,x2,..., xp} un conjunto de
vectores linealmente independientes
de un espacio vectorial E.
•
Si el vector u es C.L.de ellos, entonces los coeficientes de la combinación
lineal son únicos.
•
Todo subconjunto de {x1,x2,..., xp} es L. I.
Sea E un espacio
vectorial y {u1,u2,...,
up} L. I. de E, las
equivalen:
·
{v,u1,u2,...,
up} es L. I.
·
v no pertenece
a Env {u1,u2,..., up}
Sea {x1,x2,..., xp} un conjunto de
vectores linealmente dependientes
de un espacio vectorial E.
·
Cualquier conjunto que lo
contiene también es linealmente dependiente.
·
Un conjunto de vectores de un
espacio vectorial E es linealmente dependiente si, y sólo si, alguno de ellos
es combinación lineal de los restantes.
El conjunto {b1,b2,...,
bn} de un e. v. E es una base
de E si es un conjunto generador de E y
libre (L. I. ) (ver ejercicio 2)
Todo espacio vectorial E de generación finita, distinto de {0}
tiene una base.
Se llama dimensión de un espacio vectorial E (dim E) al número de vectores
de una base de E. Notar que dim {0} = 0.
Todas las bases de E tienen la misma dimensión.
Sea
E / dim(E)=n y E=Env{u1,u2,...,
un}. Entonces
{u1,u2,..., un} es base de E.
Sea
E un e. v. /dim(E)=n y {u1,u2,...,
un} es linealmente independiente. Entonces
{u1,u2,..., un} es base de E.
· Teorema de la base incompleta
Sea E un e. v./ dim(E)=n. Si {b1,b2,...,
bp} es un conjunto libre de E, entonces se pueden encontrar n-p
vectores de E tales que con los anteriores forman una base de E.
· Propiedades
·
Sea F un subespacio vectorial
de un e. v. E de dimensión finita y {d1,d2,...,
dp} una base de F. Entonces se puede encontrar una base de E
que contiene al conjunto {d1,d2,...,
dp}.
· Sea E un e. v. de dimensión finita. Si F es un subespacio vectorial de E, entonces
dim F £ dim E
· Suma e intersección de subespacios vectoriales
Sean F y G dos subespacios vectoriales de un espacio vectorial E. Se llama suma de F y G al conjunto:
![]()
La suma de subespacios
vectoriales es subespacio vectorial.
Se dice que la suma de F y G es directa cuando dado un vector z de F+G, se escribe de forma única como
![]()
En este caso la suma se escribe como FÅG
·
Intersección
de subespacios vectoriales
Sean F y G dos subespacios vectoriales de un espacio vectorial E. Se
llama
intersección de subespacios vectoriales de F y G al conjunto
![]()
La
intersección de subespacios vectoriales es subespacio vectorial
·
Teorema
Sean F y G dos subespacios vectoriales de un e. v. E
![]()
·
Propiedades
Sean F y G dos subespacios vectoriales de un e. v. E tal que S = F
+ G. Las siguientes condiciones son
equivalentes
·
S = F Å G
·
El vector nulo de S se
descompone de forma única como suma de los vectores nulos de F y G.
·
Si B es una base de F y D es de
G, entonces H formada por las dos bases, es base de S.
·
F Ç G = {0}
Sean F1, F2,..., Fp,
subespacios vectoriales de un espacio vectorial E, y sea
F = F1 + F2 +...+
Fp .
Las siguiente afirmaciones equivales:
· F = F1 Å F2 Å... Å Fp
![]()
· El vector nulo de F se descompone de forma única como suma de los vectores nulos de F1, F2,..., Fp.
· Si Bi es base de Fi, i=1,2,...,p; entonces la unión de todas las bases es base de F.
dim F = dim F1 + dim F2+...+ dimFp
Se cumple:

· Rango de una matriz
Sea una matriz de tamaño m´n. Se llama rango
de A (rg A) a la dimensión del
espacio fila de A (fil(A)) ó columna de A (col(A)), es decir, al número de
vectores libres (tomados por filas o por columnas).
Sean A matriz de tamaño m´n. Se verifica:
·
rg A = rg At
·
Si rg A =m Þ las filas de A son L. I.
· Si rg A =n Þ las columnas de A son L. I.
Sea A una matriz cuadrada de tamaño n´n, es equivalente:
·
Las columnas (filas) de A
generan Ân
·
Las columnas (filas) de A son
una base de Ân
·
Las columnas (filas )de A son
L. I.
· rg A = n
Mostraremos en el apartado de ejercicios
resueltos cómo calcular bases de la suma y la intersección de subespacios.
1) Dados los siguientes subconjuntos de R3 , demuestra que son subespacios vectoriales y calcula una base.

![]()
1).
El vector (0,0,0) pertenece a A pues cumple las dos condiciones:
* la segunda componente es el doble de la primera
* la tercera componente es (-3) veces la primera
2).
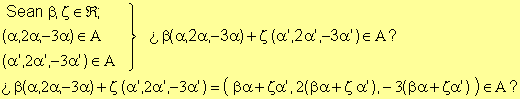
Y
este vector pertenece a A por cumplir las dos condiciones
Así pues, todo vector de A se podrá expresar:
![]()
![]()
![]()
La relación definida en B es que la primera y
segunda componentes deben ser iguales.
1). El vector (0,0,0) pertenece a B pues cumple la
condición pedida:
la primera componente y la segunda son iguales
2).
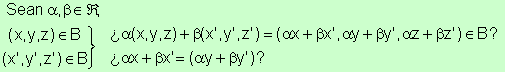
Y como x=y Þ ax=ay , por lo tanto se da.
Así pues, todo vector de B se podrá expresar:
![]()
![]()
![]()
La
relación definida en C es que la suma de las tres componentes es cero y que
la suma de la segunda con el doble de la tercera también es cero.
1).
El vector (0,0,0) está en C pues cumple las dos condiciones pedidas
2).
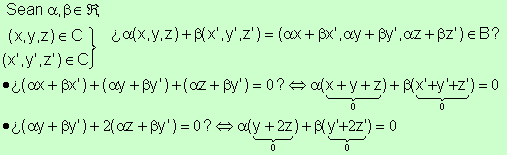
Y como x=y Þ ax=ay , por lo tanto se da.
Así pues, todo vector de B se podrá expresar:
Busquemos la base:
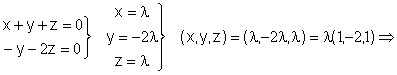
![]()
2).
a) ¿El sistema {(1,0,-1), (0,2,3), (1,4,-1)} es base de Â3?
b)
¿El sistema {(1,0,-1), (0,2,3), (1,2,2)} es base de Â3?


3)
Dados los subespacios de Â3:
S={(x,y,z) / x-2y+z=0} y T={(a,2a,a-b) / a, b Î Â}
Calcula una base para:
a)
S
b)
T
c)
S+T
d)
SÇT

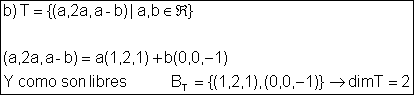

![]()
d). Para este apartado debemos tener en cuenta lo siguiente
![]()
