Cálculo de Derivadas

Índice

Atrás

·  5.5. Derivada de un producto de dos funciones

 (y escribiendo u y v, para abreviar) 

En resumen:            ®     

¤ “La derivada de un producto de dos funciones es igual a la derivada de la primera función por la segunda sin derivar, más la primera función sin derivar por la derivada de la segunda”

Ejemplos:

   a)  Sea  . Como evidentemente se trata del producto de la función exponencial natural por la función logaritmo neperiano , aplicando la regla obtenida tendremos:

   b)  Sea  , producto de una función polinómica por una exponencial de base 2. Por tanto:

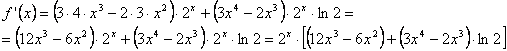
   c)  Sea , que puede considerarse producto de la función identidad  por la función raíz cuadrada . En este caso, y aplicando la regla de derivación de un producto tendremos:

No obstante, la función dada podría haber sido derivada de otra forma más fácil, si antes de derivar nos fijamos en que es un producto de dos potencias de x. Es decir:  . Y entonces la podemos derivar como una simple función potencial, obteniendo:

resultado que, si en principio parece no coincidir con el obtenido anteriormente, puede comprobarse que en realidad sí coincide, ya que

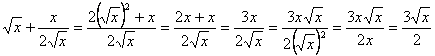
   d)  Sea  , producto de las funciones    y  , cuyas derivadas respectivas son    y  . Entonces la derivada del producto será:

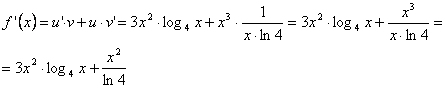
   e)  Sea , producto de las funciones    y  , cuyas derivadas respectivas son    y  . Entonces la derivada de  será:

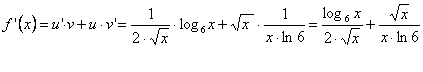
     f)  Sea  , producto de la función exponencial de base 7 por la función raíz cuadrada. Su derivada será, pues:

    g) Sea . Si la tomamos tal cual está, es evidentemente el producto de dos funciones polinómicas y como tal se podrá derivar:

         No obstante, es elemental que podríamos haber efectuado el producto de los dos polinomios antes de derivar, con lo cual hubiéramos tenido:

y ahora la derivación es mucho más fácil:

Los siete ejemplos anteriores han sido casos de productos de funciones elementales. Veamos ahora algún ejemplo de producto de funciones, una de las cuales, o ambas, sean compuestas:

   h)  Sea  . Obviamente se trata del producto de la función , una función exponencial natural de exponente la raíz cuadrada de x, por la función , función raíz cuadrada. Al derivar, teniendo en cuenta la Regla de la Cadena en la derivada de la primera función (que es compuesta), obtendremos:

   i)  Sea  , producto de la función raíz cúbica de un polinomio por el logaritmo neperiano de un polinomio. Transformando previamente la raíz cúbica en potencia de exponente fraccionario, tendremos:   , y derivando: