Cálculo de Derivadas
· 5.6. Derivada de un cociente de funciones
(y escribiendo abreviadamente u y v, como antes)
En resumen:
®
¤ “La derivada de un cociente de funciones es igual a la derivada del numerador por el denominador sin derivar, menos el numerador sin derivar por la derivada del denominador, partido todo por el cuadrado del denominador”
Ejemplos:
a) Sea
, cociente de la función logaritmo neperiano
y la función exponencial natural
.
Su derivada será:
b) Sea
.
Esta función ya la hemos derivado en el ejemplo g) del apartado de la función exponencial natural, y allí se advirtió que también se podía derivar como cociente de dos funciones, aunque no lo hicimos entonces por no haber dado todavía la regla para la derivada de un cociente. Además de que también advertimos entonces que el camino allí elegido posiblemente resulte en general más fácil para el alumno.
Vamos, pues, ahora a derivar dicha
función como cociente de dos funciones: cociente de la función
constante 
y la función exponencial compuesta
. Tendremos:
Al alumno le corresponde ahora comparar los dos procesos seguidos, sacando sus propias conclusiones respecto a la mayor o menor “facilidad” de cada uno de ellos, y tomando la decisión de derivar en lo sucesivo funciones de este tipo por el camino que considere más sencillo.
c) Sea
.
Si en el ejemplo anterior hemos dejado al libre criterio del
alumno elegir uno de los dos caminos posibles, ante un caso como éste hemos de
comentar que, si bien se podría derivar como cociente de funciones: la
función exponencial compuesta
y la función constante 
, actuando entonces en la forma
,
consideramos que el alumno no debe “complicar” inútilmente el ejercicio, ya que, si nos fijamos desde el principio, podemos observar claramente que la función dada se puede expresar inmediatamente como producto de una constante por una función, con lo que su derivación se hace, sin duda, mucho más fácil.
Queremos decir que 
, y, por tanto, ahora
con lo que el proceso ha resultado mucho más fácil.
Téngase, pues, en cuenta este “consejo” siempre que se nos presente para derivar un cociente en el que el denominador sea una constante. Y dada la importancia del caso, permítasenos insistir con un par más de ejemplos sencillos del mismo tipo:
d) Sea
. Inmediatamente escribiremos
. Y ahora derivaremos como producto de una constante por
una función:
e) Sea
. Inmediatamente escribiremos
. Y, por tanto, al derivar tendremos:
f) Sea
, típico ejemplo de función racional fraccionaria o
cociente de dos polinomios. Derivando tendremos:
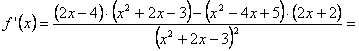
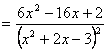
Nota: Consideramos importante advertir que, al derivar funciones racionales fraccionarias como en el caso anterior, no es en general necesario desarrollar el cuadrado (o la potencia correspondiente) del denominador. Más bien nos atreveríamos a decir que, para las aplicaciones que el alumno habrá de darles de momento a dichas derivadas, no debe “molestarse” en desarrollar dicha potencia, pues sólo le conduciría a “complicar” inútilmente el resultado obtenido.
g) Sea
, cociente entre la función raíz cuadrada y la función
logarítmica de base 6. Su
derivada, pues, será:
h) Sea
, cociente entre una función potencial y la función
logarítmica de base 4. Derivando tendremos:
i) Sea 
que, como puede observarse, es un cociente de funciones
compuestas: El numerador es la raíz cuadrada del logaritmo neperiano
, y el denominador es la función exponencial de base 2 de exponente polinómico
. Teniendo, pues, en cuenta la regla de la derivada de un
cociente de funciones y la Regla de la Cadena, tendremos:
Nota: Aun a riesgo de resultar reiterativos, hemos de insistir en que los ejemplos que hemos puesto hasta ahora se han tenido que ir ajustando a las reglas de derivación que se iban conociendo. Pero todavía nos faltan por estudiar las funciones derivadas de otras varias funciones, y, por tanto, concretamente en lo que se refiere a la derivada de un producto o de un cociente de funciones, nos reservamos el volver sobre ellas (e incluso ampliar la derivada de un producto para tres funciones) cuando hayamos aprendido a derivar las nuevas funciones que se proponen a continuación.