
 |
| 10.3 PROBLEMAS
Y EJERCICIOS PRACTICOS
Problema 2.1 Una barra de 1.25 cm de diámetro está sometida a una carga de 2500 kg. Calcular la tensión axial de la barra en megapascales (MPa).
Problema 2.2 Calcular el esfuerzo usual en ingeniería, en el SI de unidades, de una barra de 1,50 cm de diámetro que está sometida a una carga de 1200 kg.
Problema 2.3 Calcular el esfuerzo usual en ingeniería, en el SI de unidades, de una barra de 15 cm de longitud y con una sección de 5,0 mm x 10,0 mm, sometida a una carga de 4500 kg.
Problema 2.4 Calcular el esfuerzo usual en ingeniería, en el SI de unidades, de una barra de 25 cm de larga y que tiene una sección transversal de 6,0 mm x 3,0 mm, sometida a una carga de 4700 kg.
Problema 2.5 Una barra de 20 cm de largo con un diámetro de 0,30 cm es sometida a una carga de 4000 N de peso. Si el diámetro disminuye a 0,27 cm, determinar: a) El esfuerzo y la deformación usual en ingeniería para esta carga. b) El esfuerzo y la deformación verdadera para esta carga. a) Cálculo del esfuerzo, 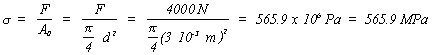 Cálculo de la deformación, L = L0 (1 + e), de donde e = L / L0 - 1 = 0.2345 b) Cálculo del esfuerzo verdadero, Cálculo de la deformación verdadera, Problema 2.6 Un acero tiene un módulo de elasticidad de 200 GPa y un límite elástico de 360 MPa. Una varilla de este material de 12 mm2 de sección y 80 cm de longitud se cuelga verticalmente con una carga en el extremo de 1800 N. a) ¿Recuperará
el alambre la longitud primitiva si le quitamos la carga?
a) Si s < L.E. se recupera.
Luego sí se recupera el alambre.b) Como estamos en la zona elástica E = s/e, luego:
c) Para que no haya deformación permanente:
Por tanto d0 = 0,00133 m |
Problema 2.7 En
un ensayo con el péndulo de Charpy la maza de 25 Kg cayó
desde una altura de 1 m y después de romper la probeta de sección
80 mm2 se elevó a 0,4 m. Calcular:
a) Energía de rotura.a) m.g (H - h) = Eabs. (25.9,8) N. (1- 0,4) m = 147 Julios b) Problema 2.8 En el ensayo de tracción de una barra de aluminio de longitud calibrada l0 = 5,00 cm y d0 = 1,30 cm. Se obtiene un registro de F = 3180 kp y Dl = 0,0175 cm. (En el L. E.). La distancia entre las marcas después de la rotura es 5,65 cm y su diámetro final 1,05 cm en la superficie de fractura. Calcular: a) Límite elástico.a) 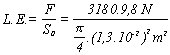
L.E. = 234,8 · 106 Pa = 234,8 MPa. b) e = Dl / l0 = 0,0175/ 5 = 3,5. 10-3
c) Alargamiento: Estricción: 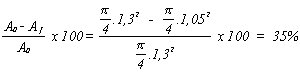 d) Al encontrarse dentro de la zona elástica,
l = l0
+ e
l0
; l = l0 (1 + e)
= 125 (1 + 2,98. 10-3);
Problema 2.9 Calcular en un ensayo Brinell: a) La dureza de un acero al carbono y su resistencia aproximada a la rotura por tracción. Se utilizó bola de 10 mm y carga de 3000 kp, obteniéndose una huella de 4 mm de diámetro.a) En el método Brinell, la dureza se obtiene presionando con una bola de acero, de diámetro D, con una fuerza P, obteniendo una huella de un casquete esférico de diámetro d, figura 2.6. El número de dureza Brinell es: Conocido el número de dureza Brinell HB, se puede calcular, de forma aproximada, la resistencia a la rotura, por tracción, de algunos materiales, mediante la relación sR = m HB + n, donde las constantes m y n dependen del material. En los aceros al carbono ordinarios, en estado bruto de laminado o recocido, la relación es, de acuerdo con la cuestión 30: Luego: b) Teniendo en cuenta que la constante de ensayo, Ce, es la relación entre las cargas aplicadas y el diámetro de la bola al cuadrado, Problema 2.10 Determinar la carga que, aplicada en un ensayo de dureza Brinell con bola de 5 mm de diámetro produciría en la probeta de un material (HB 40) una huella de 1.2 mm de diámetro. ¿Cuál es la constante de ensayo? de donde P = 45.9 kp La constante de ensayo será, Problema 2.11 Para realizar un ensayo de dureza Brinell en un acero se utiliza bola de 5 mm, obteniéndose una huella de 2 mm de diámetro. Calcular: a) Carga utilizadaa) La constante del ensayo para los aceros es Ce = 30, con lo que, P = Ce D2 = 30 x 52 = 750 kp b) La dureza se obtendrá mediante la expresión:
c) De acuerdo con la expresión que relaciona la dureza Brinell con la carga de rotura,
|
|
|
|
|
 |