
 |
| Problema 2.12
En un ensayo de dureza Vickers se ha utilizado una carga de 30 kp, obteniéndose
0,320 y 0,324 mm para las diagonales de la huella. Calcúlese la
dureza.
HV = P/S = 2P sen 68°/d2 = 1,8544 P/d2 Siendo d la diagonal de la huella. Si las diagonales son distintas se toma la media aritmética. d = (d1 + d2)/2
Problema 2.13 La escala del reloj comparador en un durómetro Rockwell está dividida en 100 partes, correspondiendo a un total de 1 mm. teniendo en cuenta que la relación entre las indicaciones del reloj comparador y el movimiento de la punta de diamante es de 5:1, determínese: a) La profundidad que corresponde a cada división del comparador y al total de la escala.a) A la vista de la relación entre las indicaciones del reloj y el movimiento de la punta del cono de diamante, cada división del reloj corresponde a: 1/5 · 1/100 = 1/500 mm = 2 micras, que es la equivalencia
en profundidad de cada unidad Rockwell.
b) Puesto que HRc = 100 - e, será: Problema 2.14 Una
probeta de acero Cr-V (E = 210 GN m-2), de 100 mm de longitud requiere
una fuerza de 4000 daN para producirle una deformación total de
0,125 mm y 14000 daN para ocasionar la rotura. Con estos datos, se pide
la penetración que producirá una bola en un ensayo de dureza
HRb.
con lo que la sección de la probeta será, considerando s = F / S,
de manera que la carga de rotura será: y con ello, la dureza Brinell podrá expresarse como:
y relacionando la dureza Rockwell con la dureza Brinell tendríamos:
con lo que podremos calcular ya la penetración de la bola, mediante la expresión:
Problema 2.15 Un componente estructural de chapa de un diseño de ingeniería debe soportar 207 MPa de tensión. Si se usa una aleación de aluminio 2024-T851 para esta aplicación, ¿cuál es el mayor tamaño de grieta que este material puede soportar? Considerar el factor de intensidad de tensiones, KIC = 26,4 MPa.m1/2
con o cual la grieta tendrá unas dimensiones de: 5.177 mm si es exterior, y,Problema 2.16 ¿Cuál es el tamaño más grande (en mm) de una grieta interna que una lámina gruesa de aleación de aluminio 7178-T651 puede soportar aplicándole un esfuerzo: a) 3/4 del esfuerzo de fluencia;a) Los 3/4 del esfuerzo de fluencia será, 570 x 0.75 = 427.5 MPa, por lo que:
b) La mitad del esfuerzo de fluencia será igual a 285 MPa, con lo que:
|
| Problema 2.17
El máximo esfuerzo que actúa en la superficie de una barra
cilíndrica cuando se aplica una fuerza que la flexiona en un extremo
es:
Esfuerzo aplicado (Mpa) 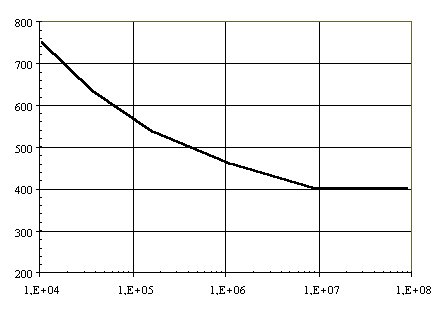
Número de ciclos de esfuerzo Diagrama de esfuerzo y número de ciclos a la fractura de un acero de herramientas donde: l es la longitud de la barra, F es la carga, y, d el diámetro. Se aplica una fuerza de 2900 N. a una barra de acero para herramientas que gira a 3000 ciclos por minuto. La barra tiene un diámetro de 2,5 cm. y una longitud de 30 cm. a) Determinar el tiempo tras el cual la barra falla.a) 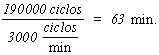
Esfuerzo aplicado (Mpa) 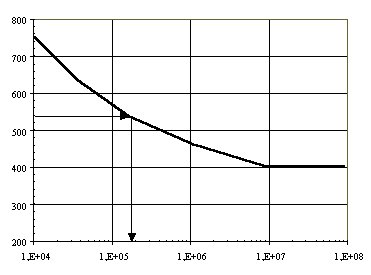
Número de ciclos de esfuerzo Problema 2.18 Determina el modelo de resistencia, exponencial amortiguado, a la rotura por fatiga a tracción de un material del que se disponen los sigueintes datos: . Tensión de rotura: 750 MPa.La tensión de rotura corresponde a la carga para un ciclo, así como el límite de fatiga sería el correspondiente a la carga, 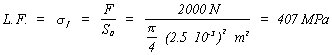 Considerando la expresión del modelo analítico correspondiente a la resistencia a fatiga,
con los valores analíticos s0 = 750 MPa, sf = 407 MPa, y s = 577 MPa cuando n = 103 ciclos. Sustituyendo en el modelo general 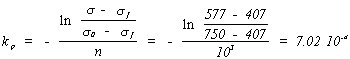 El modelo de resistencia será, por lo tanto:
|
|
|
|
|
 |