Para efectuar pruebas de tracción que permitan caracterizar dicho acero, dispone de una prensa de ensayos con Fmax = 50 KN. Las probetas de tracción deben ser normalizadas según UNE 7262, que exige se cumpla la relación:

a) Determine cual de las siguientes dimensiones de probeta resulta adecuada para poder realizar el ensayo en su máquina:

probeta tipo 1: d0 =  8 mm S0 = 50,26 mm2
probeta tipo 2: d0 = 10 mm S0 = 78,50 mm2
probeta tipo 3: d0 = 12 mm S0 = 113   mm2

a)  En primer lugar deberemos comprobar cuales son los esfuerzos necesarios para romper las probetas de los diferentes materiales, tal como aparece reflejado en la tabla siguiente:
 

Tal como se aprecia en la tabla debe seleccionarse las probetas del tipo 1 puesto que las demás superan la capacidad del equipo de que se dispone. Las dimensiones de las probetas serán por tanto: d0 = 8 mm, S0 = 50.26 mm2, L0 = 40 mm

b) Para los datos suministrados por la gráfica, se obtiene:
   b1) Carga de rotura, R = 34340 N / 50.26 mm2 = 683 MPa
   b2) Límite elástico, LE = 16100 N / 50.26 mm2 = 320 MPa
   b3) Alargamiento, en % = (Lf - L0) / L0 = 7.5 / 40 = 18.75 %
   b4) Estricción, S = (S0 - Sr) / S0 = 20.07 / 50.26 = 39.93 %
   b5) Corresponde a un acero F-1140, al corresponderle tanto la carga de rotura como el límite elástico superior al del acero F-1130, sin embargo el alargamiento es bastante superior también al del acero F-1150 que tendría mayor límite de elasticidad.

Problema 2.20 Una barra cilíndrica de 380 mm de longitud y un diámetro de 10 mm, es sometida a esfuerzos de tracción. Si la barra no debe experimentar, ni deformación plástica ni elongación superior a 0.9 mm, cuando se aplica una carga de 24500 N, ¿cual de los cuatro materiales de la tabla siguiente son posibles candidatos?. Justificar la respuesta.
 

En primer lugar calcularemos la tensión correspondiente a la carga aplicada de 24500 N.

por lo tanto, para que la barra no experimente deformación plástica se descarta la aleación de aluminio y el cobre.
Para que la elongación no sea superior a 0.9 mm, deberá cumplirse que el módulo elástico sea superior a:

por lo que sólo el acero cumple las condiciones impuestas.

Problema 2.21 A partir de la curva tensión-deformación de la probeta de latón mostrada en la figura, determinar:
a) El módulo de elasticidad.
b) El límite elástico para una deformación del 0.002.
c) La carga máxima que puede soportar una probeta cilíndrica con un diámetro original de 11.5 mm.
d) El cambio en la longitud de una probeta originalmente de longitud 125 mm que es sometida a una tensión de tracción de 375 MPa.

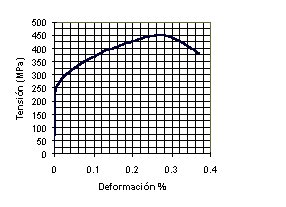b)  Leyendo la tensión directamente en el diagrama para una deformación del 0.2%, ésta es: 240 Mpa

c)   F = s x S

F = 450 Mpa x 103.9 mm2 = 46.7 kN

d) Para la tensión de 375 Mpa leemos en el diagrama que la deformación obtenida es de 0.11%, por lo que la longitud de la probeta a esa tensión será:

por lo que el cambio de longitud, DL será de 13.75 mm.

Problema 2.22 Una barra cilíndrica de 120 mm de longitud y con un diámetro de 15.0 mm se deforma usando una carga de 35 kN. No debe experimentar deformación plástica ni tampoco el diámetro debe reducirse en más de 1.2 · 10-2 mm. ¿Cuales de los materiales, tabulados a continuación, son posibles candidatos?. Justificar la respuesta
 

Para no experimentar deformación plástica, el límite elástico del material debe ser mayor que:

y por tanto, la aleación de magnesio no sirve.

Se pide además que D? < 1.2 x 10-2 mm. Considerando que:

calculamos la disminución de diámetro obteniendo los datos de la tabla:
 

por lo que sólo cumple el acero.

Problema 2.23 Para un determinado latón, la tensión a la cual comienza la deformación plástica es 345 MPa y el módulo de elasticidad es 103 GPa. Calcular:

a) ¿Cual es el máximo esfuerzo que puede aplicarse a una probeta con una sección de 13 mm de diámetro, sin que se produzca la deformación plástica?

b) Si la longitud original de la probeta es de 75 mm, ¿cual es la máxima longitud que puede ser estirada sin causar deformación plástica? 
L.E. = 345 MPa
E = 103 GPa

a) ? = 13 m.m.

a) De la tabla calculamos, para la sección de la estructura, tanto el límite de elasticidad como la carga de rotura,

LEmin = 460 kN / 15 · 10-4 m2 = 306,7 MPa
Rmin = 1010 kN / 15 · 10-4 m2 = 673 MPa

b) Si seleccionáramos el acero inoxidable 304, como material para la estructura, las dimensiones de este deberían cumplir la doble condición, es decir:

Para el límite elástico, Smin = 460 kN / 205 MPa = 22,44 · 10-4 m2
Para la carga de rotura, Smin = 1010 kN / 515 MPa = 19,61 · 10-4 m2