
 |
| 11.4. PROBLEMAS Y EJERCICIOS PRACTICOS |
| Problema 3.1 La
distancia entre los planos de índices (110) en una red cúbica
centrada c.c. es d110 = 2.65 Å.
Calcular: a) La constante reticular.a) En las redes cúbicas, los planos de índices (110) son planos que pasan por una arista y la diagonal de una cara, tal como se muestra en la figura. |
 |
| Para esta familia de
planos, la relación geométrica entre la distancia dhkl de
otro plano paralelo y la constante reticular vale:
de donde a = dhkl ( h2 + k2 + l2)1/2 b) En una red c.c. la diagonal del cubo es compacta, es decir, los átomos de las esquinas y el central están tocándose. Por lo tanto, y asumiendo un modelo de esferas duras, la diagonal del cubo, cuya longitud es a?3, tiene la misma longitud que 4 radios atómicos (intersecta completamente al átomo central y hasta el centro a los dos átomos de las esquinas opuestas). Esto es:
|
| Problema 3.2 Calcular
la densidad teórica del hierro a temperatura ambiente, sabiendo
que presenta red c.c. con parámetro reticular a = 2.866 Å.
Peso atómico de Fe: 55.847.
Nota: Cte de Avogadro: 6.0248 1023 átomos/mol. El número de átomos por celda en la red c.c. es de 1 + 8 (1/8) = 2 átomos/celda.Problema 3.3 Se pretende determinar qué tipo de pigmento blanco se ha utilizado como colorante en un termoplástico. Para ello se examina una muestra pulverizada con difracción de rayos X, empleando radiación Cu Ka de l = 1.541Å. Se obtuvo un espectro de difracción con picos en los ángulos 2q : Pico 1: 31.72°, Pico 2: 57.73°, Pico 3: 39.12°. a) Determinar el tipo de pigmento utilizado.NOTA: Se dispone de las fichas JCPDS para los diversos pigmentos que se consideran posibles, de las que se extraen los datos sobre las tres distancias más significativas siguientes:
a) A partir de los valores de ángulos 2q y de la ecuación de Bragg, se determinan las distancias dhkl correspondientes a cada pico.
Valores que coinciden significativamente con los correspondientes al producto PbO.TiO2. b) Es evidente que un análisis químico informaría de la presencia de Pb y Ti. Pero no podría discernir si corresponden a un producto dado, como el PbO.TiO2 o bien es que existe una mezcla de óxidos de TiO2 y Pb2O3. El análisis químico resulta, por tanto, insuficiente para identificar las estructuras cristalinas presentes. |
| Problema 3.4 Una
muestra de aluminio finamente pulverizado se somete a un ensayo de difracción
de rayos X en un difractómetro de polvos. Se utilizó radiación
monocromática Cu Ka
con longitud de onda l
= 1.541 Å. El espectro obtenido se muestra en la figura siguiente.
Se pide determinar: a) distancias interplanares
que producen difracción.
|
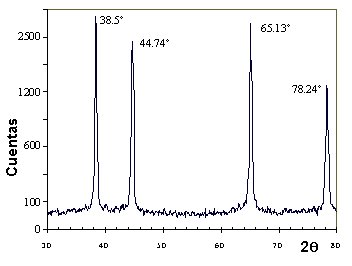 |
a) Cálculo de
distancias interplanares que producen difracción. Se determina en
primer lugar los ángulos 2q
en los que aparece difracción.
A partir de la Ley de Bragg, l = 2 d senq, puede obtenerse los valores de d: d= l / 2 senq, donde l = 1.541 Å.
b) Cálculo del
parámetro reticular. En las redes cúbicas, la segunda raya
del espectro corresponde a la difracción sobre planos de índices
(200).
dhkl = a ( h2 + k2 + l2)-1/2 c) Determinación del tipo de red. En la red c.c. sólo son observables los planos que cumplen: h + k + l = 2 n En la red c.c.c. sólo son observables los planos donde todos los índices son pares, o impares, es decir: h,k,l = 2nSegún estas reglas, los espectros característicos de cada red son:
En la estructura c.c., se cumple: mientras que en la red c.c.c., se cumple: En nuestro caso: luego se trata de una red c.c.c. d) Determinación del radio atómico del aluminio. En las redes c.c.c, la dirección densa es la diagonal de una cara. Por lo tanto: Problema 3.5 En una muestra de cobre se aprecia mediante observación metalográfica la existencia de un precipitado. Para identificarlo, se somete la muestra a un ensayo de difracción de rayos X. Se sabe que el cobre presenta estructura c.c.c con parámetro reticular a = 3.616 Å. Determinar si un pico para d = 1.419 Å corresponde al cobre o al precipitado. Por ser c.c.c., el cobre presentará difracción en planos hkl que cumplan: h,k,l = 2nEs decir, para planos, en orden creciente, de índices: (111), (200), (220), (311), (222)... Para cada uno de estos planos puede calcularse la distancia interplanar, dhkl, según la expresión: por lo que resulta evidente que d = 1.419 Å no puede corresponder a difracción sobre planos del cobre, confirmando la existencia de otras fases diferentes en la estructura. Problema 3.6 Caracterización
mecánica de fases mediante microdurezas.
a) Determinar cual
es el rango aproximado de carga que deberá utilizarse en el microdurómetro
para asegurar que las huellas de microdureza afectan a un solo grano.
b) Se realiza el
ensayo sobre distintos granos, tomando medidas exclusivamente de las huellas
que afectan a un solo grano o fase.
|
|
|
|
|
|
|
435 160 250 168 428 389 171 |
Interior Interior Borde Interior Interior Interior Interior |
A B A + B B A B (+ A) B |
Huella sobre dos fases
Huella sobre B. Posible A debajo |
| ¿Cual es la microdureza
de cada una de las fases presentes?
1) Selección
de cargas
HV = 1.854 P(kg) / d2(mm2) = 1854 P(g) / d2(mm2) podemos obtener P(g),
con la condición de que d sea menor que el tamaño del grano.
P(g) = HV ( d2 / 1854 ) = 360 ( 2500 / 1854 ) = 485 g por lo que una carga de 500 g constituye la solución más adecuada para abordar el estudio.
Una vez desestimados los valores de 250 y 389, que claramente no corresponden a uno u otro tipo de grano, se calculan las propiedades para cada fase: Dureza fase A : (420 + 435 + 428) / 3 = 428 HV |
|
|
|
|
 |