Unidad 3. Estructura de los materiales. Imperfecciones
11- Cuestiones propuestas por las experiencias
Anterior                                                            Siguiente
Problema 3.7 Una muestra de material finamente pulverizado se somete a un ensayo de difracción de rayos X en un difractómetro de polvos. Para ello, se emplea una radiación monocromática Cu Ka con longitud de onda l = 1.541 Å. El espectro obtenido se muestra en la figura siguiente.

Se pide:
 a) Calcular las distancias de los planos que producen difracción, empleando para ello la ley de Bragg.
 b) Calcular el parámetro reticular, sabiendo que es una red cúbica.
 c) Determinar si se trata de una red C.C. o C.C.C.
 d) Sabiendo que la densidad de la muestra es de 8.01 g/cm3, calcular el peso atómico.
a) Cálculo de distancias interplanares que producen difracción. Se determina en primer lugar los ángulos 2q en los que aparece difracción.
 
Picos 2q 42.80 49.30 72.30
Angulos q 21.40 24.65 36.15
Sen q .3649 .4171 .5899

A partir de la Ley de Bragg, l = 2 d senq, puede obtenerse los valores de d:

d= l / 2 senq,          donde l = 1.541 Å.

d (Å)
2.11
1.85
1.31

b) Cálculo del parámetro reticular. En las redes cúbicas, la segunda raya del espectro corresponde a la difracción sobre planos de índices (200).

Sabiendo que para las redes cúbicas, la distancia entre planos de índices hkl vale:

dhkl = a  ( h2 + k2 + l2)-1/2

para los planos (200) se tiene:
 d(200) = 1.85 Å = a/2,
de donde
 a = 3.70 Å

c) Determinación del tipo de red.
En la estructura c.c., se cumple: 

mientras que en la red c.c.c., se cumple:

En nuestro caso:

luego se trata de una red c.c.c.

d) Calcular el peso atómico. En las redes c.c.c, el número de átomos por celda es:

6 (1/2) + 8 (1/8) = 4 átomos/celda.

y el volumen de la celda será:
 a3 = (3.70 10-8 cm)3 = 5.065 10-23 cm3

sabiendo que la densidad = 8.01 g/cm3 = masa / volumen, el peso atómico será:

Problema 3.8 En el espectro de difracción de rayos X de la figura, aparecen los picos correspondientes a una mezcla de dos materiales metálicos, que se sabe presentan el mismo sistema cristalino cúbico.
Para la realización del espectro, se ha empleado radiación monocromático Cu Ka con una longitud de onda l = 1.541 A. Calcular:

 a) Las distancias interplanares correspondientes a cada metal.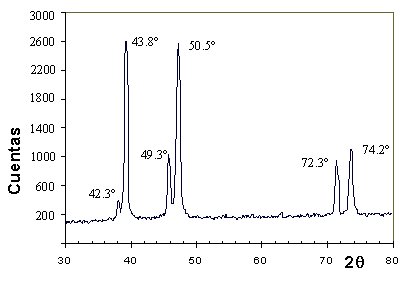
 b) Calcular el parámetro reticular de cada metal.
 c) Determinar el tipo de red cúbica de la que se trata.
a) Las distancias interplanares se obtienen aplicando la ley de Bragg, l = 2 d senq, de forma que:

d= l / 2 senq,          donde l = 1.541 Å.

Picos 2q 42.30 43.40 49.30 50.50 72.30 74.20
Angulos q 21.15 21.70 24.65 25.25 36.15 37.10
Sen q .3608 .3697 .4171 .4266 .5899 .6032
d (Å) 2.136 2.084 1.847 1.806 1.306 1.277

Las distancias interplanares serán:   del metal A, 2.136, 1.847 y 1.306
del metal B, 2.084, 1.806 y 1.277

b) Cálculo de los parámetros reticulares. Como los dos metales presentan el mismo sistema cristalino cúbico, sabemos que:

que para los planos (200) correspondientes a la segunda raya, tendremos:

 d(200) = a/2,
de donde:
 para el metal A, a = 2 x 1.847 = 3.694 Å
 para el metal B, a = 2 x 1.806 = 3.612 Å
c) Determinación del tipo de red de ambos metales
En ambos casos, al ser del mismo sistema cristalino, deberemos obtener la relación entre el segundo y primer pico de manera que:
 
 
Metal A
Metal B
0.864
0.867

que presentan valores similares a 0.860 correspondiente a la relación para estructuras cúbicas centradas en las caras, luego se trata de redes C.C.C.
Problema 3.9 Calcular la densidad del níquel sabiendo que su estructura cristalina es una cúbica centrada en caras , su radio atómico es de 0.125 nm y su peso atómico de 58.68 g/mol.
Número de Avogadro = 6.023 1023 at./mol

 Al tener el níquel una estructura c.c.c., n = 4 átomos, por lo que Vceld será:

Problema 3.10 En una chapa de latón (Cu-30%Zn) se pretende depositar un recubrimiento Sn-Ag, para lo cual se necesita proporcionar al metal base un recubrimiento previo de cobre. El análisis por difracción de rayos X del conjunto, empleando una radiación Ka  del Cu con una longitud de onda de 1.541 Å, presenta picos en los siguientes ángulos 2q: 37.4°, 39.4°, 42.1°, 43.0°, 49.0°, 50.1°, 51.6°, 72.0° y 73.9°.

Disponemos de las fichas JCPDS de los tres materiales cuyos principales datos se recogen en la tabla siguiente:

Material 
Distancias interplanares (Å)
Pico 1
Pico 2
Pico 3
Latón (Cu-30%Zn)
2.13
1.85
1.31
Cobre
2.09
1.81
1.28
Ag3Sn
2.39
2.28
1.76
a) Identificar a que material corresponde cada uno de los picos detectados, sabiendo que se cumple la ley de Bragg, donde:
l = 2 d sen q
Identificados los tres picos que corresponden al cobre, determinar:
b) El parámetro reticular, sabiendo que su estructura es cúbica.
c) Si se trata de una red C.C. o C.C.C.
d) Sabiendo que el latón presenta una estructura cristalina idéntica al cobre, calcular el aumento en el parámetro reticular que supone la adición del 30% de zinc al cobre.


a)  Los diferentes datos del espectro, y la asignación de picos es la que se recoge en la tabla siguiente, tras aplicar la ley de Bragg.

2q
q
sen q
dhkl
Asignación material
37.4
39.4
42.1
43.0
49.0
50.1
51.6
72.0
73.9
18.7
19.7
21.05
21.5
24.5
25.05
25.8
36.0
36.95
0.3206
0.3370
0.3592
0.3665
0.4146
0.4235
0.4352
0.5878
0.6011
2.4032
2.2857
2.1451
2.1023
1.8580
1.8198
1.7703
1.3109
1 - Ag3Sn
2 - Ag3Sn
1 - Latón
1 - Cobre
2 - Latón
2 - Cobre
3 - Ag3Sn
3 - Latón
3 - Cobre

b)  Cuando la red es cúbica, el segundo pico corresponde al plano (2 0 0)por lo que considerando la relación: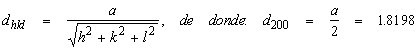

con lo que el parámetro fundamental de la celdilla será: a = 3.6395 Å

c)  Si la red es C.C., tendremos: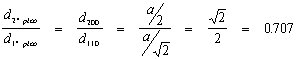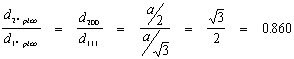

Si la red es C.C.C., entonces:
En nuestro caso:

y por lo tanto es una red C.C.C.

d) En el caso del latón, siendo una red similar a la del cobre, tendremos que el parámetro fundamental de la celdilla será:

a = 2 d2ª pico = 2 · 1.8580 = 3.7160 Å

y por lo tanto, el aumento del parámetro debido a la adición de zinc, vendrá expresado por:

Problema 3.11   El zinc cristaliza en el sistema hexagonal compacto. Determínense los parámetros de la red cristalina si su densidad es de 7136 kg/m3 y su masa atómica, Ma, 65.38 g..
 Número de Avogadro = 6.023 1023 at./mol
 Relación entre parámetros reticulares, 
El número de átomos de la red hexagonal compacta será:
12 · 1/6 (vértices) + 2 · ½ (caras) + 3 (interior) = 6
y el volumen de la celdilla, considerando la densidad del material será:

siendo:

y la superficie de la base es la superficie de un hexágono = (perímetro x apotema) / 2, 
o lo que es lo mismo:

con lo que, siendo c = ?3 a, el volumen será:

y de aquí:

y                                                                  c = 4.71 · 10-10 m = 4.71 Å

Problema 3.12 Una radiación monocromática, de una longitud de onda de 0.1542 nm, incide sobre el cromo (c.c.), que tiene un radio atómico de 0.1249 nm, calcular para el conjunto de planos (211):
 a) la distancia interplanar, y,
 b) el ángulo de difracción.

a)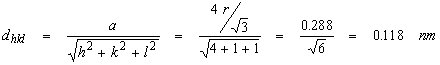

b)  El valor de q se puede calcular mediante la ley de Bragg, con n = 1.


con lo que  q = 40.88°
El ángulo de difracción será, por tanto:              2 q = 81.76°

 
Menú Principal
Menú Unidad 3
Arriba