Calcular: 
    a) Si cristaliza en un sistema cúbico, su parámetro fundamental de celdilla.
    b) ¿De que sistema se trata? 

 a)  d(200)        2º pico en redes cúbicas

        (C.C.C.)

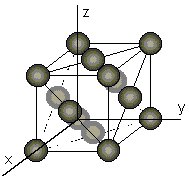
Problema 3.14 El cobre tiene una estructura cúbica centrada en las caras, un radio atómico de 0.1278 nm y una masa atómica de 63.54 g/mol. Considerando a los átomos como esferas rígidas en contacto a lo largo de las diagonales de la celdilla unidad, calcular:

a) la densidad teórica 
b) El radio del mayor hueco de tipo intersticial que encontramos, sabiendo que se encuentra en las posiciones cristalinas del tipo (½, 0, 0) (0, ½, 0) (0, 0, ½) 

Problema 3.15 En la figura siguiente se muestran los tres primeros planos que proporcionan picos de difracción de rayos X para el aluminio, con radiación Cu Ka, l = 0,1542 nm

a) Dibújese cada plano, contenido en la celda unitaria de la estructura cúbico centrado en las caras, y señálense las posiciones atómicas dentro de los planos. (realícese, mejor, un dibujo separado para cada plano)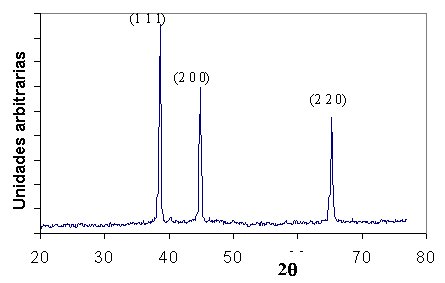

b) Empleando la ley de Bragg, d = nl/2 senq, calcúlese los ángulos de difracción (2q) para estos picos, sabiendo que el lado de la celdilla es a = 0,404 nm.

a)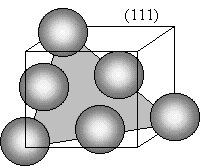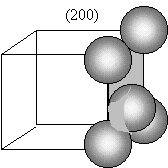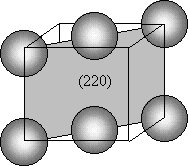

 b) Empleando la ley de Bragg,

para n=1, y para l = 0,1542 nm

Problema 3.16 El hierro puro presenta las formas alotrópicas: Fe a (c.c.) de parámetro reticular a = 2.90 · 10-10 m y a 910°C se transforma en Fe g (c.c.c.) de parámetro reticular a= 3.65 · 10-10 m. Se pide: 

a) Demostrar si dilata o contrae al pasar de hierro a a hierro g. 
b) Calcular las variaciones de densidad de cada forma alotrópica sabiendo que la masa atómica del hierro es 55.85.
El número de Avogadro, NA es igual a 6.02 · 1023. 

Para el Fe a :  V = 2 · (2.90 · 10-10)3 = 48.778 · 10-30 m3,
Mientras que para el Fe g tendremos, V = (3.65 · 10-10)3 = 48.627 · 10-30 m3.
Que corresponde a una contracción.