·  5.8. Derivada de una función potencial-exponencial

         Como su nombre indica, nos referimos a funciones que son “a la vez” potenciales y exponenciales por aparecer la variable independiente x tanto en la base como en el exponente de la potencia.

         No creemos necesario insistir mucho sobre este tipo de funciones, pero, no obstante, estudiaremos dos ejemplos fáciles.

   a)  El más sencillo y “típico” es la función  , y para su derivación dijimos en su momento que habría que utilizar el método de la derivada logarítmica. Como el proceso ya se explicó en el apartado correspondiente, nos limitaremos ahora a aplicarlo a este caso. Tendremos:

            ®      ®    

          y derivando ambos miembros   ® 

         de donde  

   b)     ®      ®      ®

        ®      ® 

        ®
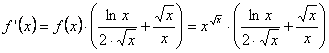