·  5.7.5. Derivada de la función inversa de una función

        Dada una función    que tiene derivada no nula en , si admite función inversa   en un cierto entorno de ,  entonces  es derivable en   , siendo   , es decir,

 ¨  Sólo es necesario tomar límites cuando   en 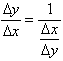   , ya que, si  ,  también    al ser  f  derivable, y, por tanto, continua en , por lo cual 

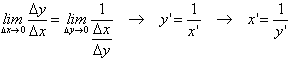
Ejemplo:    

 · 5.7.6. Derivada de la función arcoseno                                              

¤ “La derivada de arcoseno de x es igual a la unidad partida por la raíz cuadrada de uno menos el cuadrado de x”

 Incluyendo la Regla de la Cadena:  

Ejemplos:

   a)  Si , clara función compuesta de otras dos (arcoseno de la raíz cuadrada), su derivada será:

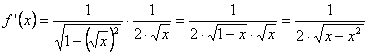
  b)  Si , también composición de dos funciones: arcoseno de un cociente (o de una función racional fraccionaria), derivando obtendremos:

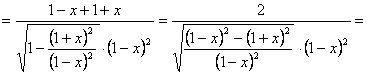
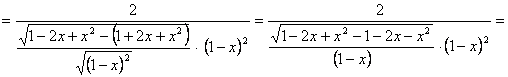
          (este último paso, para mayor “claridad”)

·  5.7.7. Derivada de la función arcocoseno                                                     

¤ “La derivada de arcocoseno es la opuesta de la de arcoseno”

Incluyendo la Regla de la Cadena:     

Ejemplos: 

   a)  Si , producto de una constante por la función compuesta arcocoseno del logaritmo neperiano, derivando tendremos:

    b)  Si , función compuesta de tres funciones (arcocoseno de una exponencial natural de exponente polinómico), su derivada será:

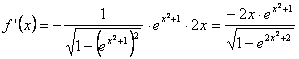
·  5.7.8. Derivada de la función arcotangente   

¤ “La derivada de arcotangente de x es igual a la unidad partida por uno más el cuadrado de x”

Incluyendo la Regla de la Cadena:     

Ejemplos:

   a)  Si  , función compuesta de tres funciones (arcotangente de la raíz cuadrada de un polinomio), su derivada es:

   b)  Si  , arcotangente de una función racional fraccionaria (o de un cociente), derivando obtendremos:

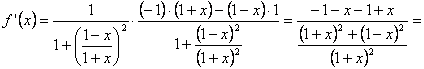
    c)  Si  se trata de la composición de tres funciones:,  y . Es decir, se trata del arcotangente del coseno del seno. Por tanto, al derivar obtendremos        

· 5.7.9. Derivada de la función arcocotangente                                                        

¤ “La derivada de arcocotangente es la opuesta de la de arcotangente”

 Incluyendo la Regla de la Cadena:     

Ejemplos:

   a)  Si  escribiremos primero , y derivando ahora como producto de una constante por una función compuesta de tres funciones (arcocotangente de la raíz cuadrada de un polinomio) se tendrá:

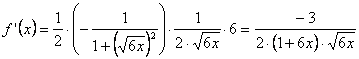
    b)  Si , producto de una constante por una función compuesta (arcocotangente de una exponencial de base 2), su derivada es:

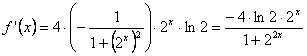
    c)  Si  se trata del arcocotangente de una exponencial de base 7, luego derivando:
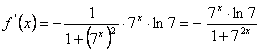