7.13. Desarrollo de un polinomio en series de potencias: Fórmulas de Taylor y MacLaurin.

        En este apartado veremos cómo utilizar polinomios especiales para el cálculo aproximado de funciones. Es necesario conocer el significado y valor del símbolo “factorial de n”, n!, ya que simplifica en gran medida las fórmulas.

Recordemos que , es decir,

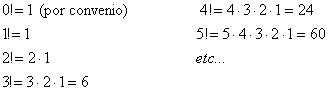
·  Desarrollo de un polinomio según las potencias de

Antes de definir el desarrollo de una función cualquiera en serie de potencias, partimos de  un polinomio  de grado n, en el que tratamos de calcular los coeficientes  para que se verifique:

es decir, ordenar el polinomio  según las potencias de .

Para el cálculo de dichos coeficientes indeterminados, hallaremos las sucesivas derivadas de P(x)  

y el resto de derivadas son nulas.

 Para , las igualdades anteriores quedarán como sigue:

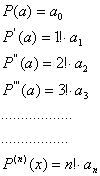
Luego tendremos que:

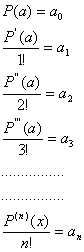
Dichas constantes sustituidas en el desarrollo de  quedará:

Ejemplo:

   a)  Ordenar el polinomio , según las potencias de .

Solución:

Como  es un polinomio de cuarto grado, tendremos:

        Calculamos ahora las derivadas sucesivas:

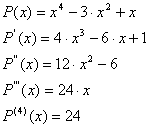
Sustituimos a continuación el valor  en las derivadas y obtenemos:

Por lo tanto:

Ejemplo:

   b)  Ordenar el polinomio , según las potencias de .

Solución:

Como  es un polinomio de quinto grado, tendremos:

Calculamos ahora las derivadas sucesivas:

Sustituimos a continuación el valor  en las derivadas y obtenemos:

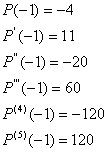
Por lo tanto: