Interconexión genérica realimentada de sistemas dinámicos (star product), fórmulas en representación interna

Antonio Sala, UPV

Dificultad: **** ,       Relevancia: ,      Duración: 18:21

Resumen:

Este vídeo plantea cómo obtener las ecuaciones de bucle cerrado de una interconexión entre dos sistemas multivariables dada por el diagrama de bloques:

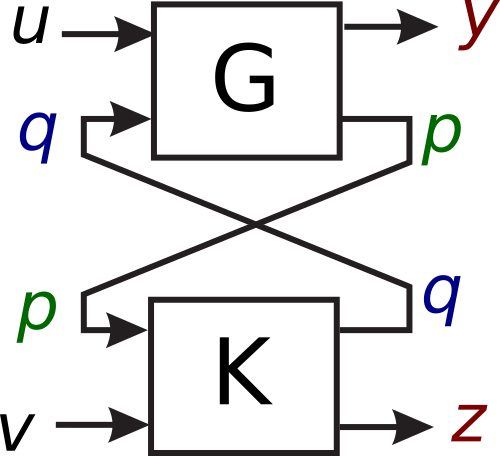
para el caso de que $G$ y $K$ estén disponibles en representación interna normalizada. En el desarrollo, las matrices de las representaciones internas se particionan adecuadamente con dimensiones compatibles a cada grupo de entradas y salidas. El resultado es un sistema en bucle cerrado cuyas entradas son $(u,v)$ y cuyas salidas son $(y,z)$, habiendo eliminado $p$ y $q$, aunque realmente en las manipulaciones intermedias, se obtiene su ecuación de salida involucrando a los estados $x_G$ y $x_K$ y las entradas $(u,v)$, por lo que podría ser utilizada si así se desease.

Tras resolver y obtener la fórmula de interconexión, se constata que es necesario que determinada matriz sea invertible. Ello, por tanto, requiere definir qué se entiende por una interconexión “bien planteada” precisamente en términos de invertibilidad de dicha matriz. El problema puede manifestarse cuando existen bucles algebraicos entre $p$ y $q$.

Se pone un ejemplo de un bucle cerrado que NO está bien planteado y, por tanto, da lugar a matrices de transferencia entre algunas de las variables que NO son realizables y, por tanto, no admiten una representación interna con las fórmulas antes desarrolladas. Esta situación de bucles mal planteados debería ser evitada en la práctica.

El ejemplo de Matlab en la segunda mitad del vídeo [estint] también ilustra esta interconexión y los problemas que pueden ocurrir al interconectar procesos inestables con procesos de fase no mínima.

Colección completa [VER]:

• Anterior   Inversa de sistemas dinámicos en representación interna

• Siguiente Interconexión de sistemas (representación en variables de estado): estabilidad interna