DIAGONALIZACIÓN DE MATRICES
· Diagonalización de matrices reales
· Diagonalización de matrices reales simétricas
|
Temas relacionados: |
Sea
A una matriz de tamaño n´n:
i).
Un número real l
es un valor propio de A si para algún vector no nulo u
de Ân:
|
Au = lu |
ii)
El vector no nulo u que satisface
dicha ecuación, se llama vector propio de A asociado al valor propio l.
|
qA(l) = det(lI-A) |
·
Multiplicidad
algebraica
Se llama multiplicidad algebraica de un
valor propio, a su multiplicidad como raíz del polinomio característico, es
decir, al número de veces que aparece como raíz de dicho polinomio.
·
Multiplicidad geométrica
Se
llama multiplicidad geométrica a la dimensión del subespacio propio EA(l), es decir al conjunto de vectores asociados a
un valor propio l
concreto (incluyendo el vector nulo).
Sea A una matriz cuadrada. Equivalen:
·
l es un valor propio de A.
·
El
subespacio vectorial asociado a l es distinto de 0.
· La matriz lI – A no es invertible.
Sea
A una matriz cuadrada. Entonces:
· Un vector propio de A está asociado a un único valor propio.
·
A
y AT tienen los mismos valores propios con las mismas
multiplicidades algebraicas (pero no los mismos vectores propios)
·
Si l es valor propio de A y k³1, entonces lk es un valor propio de Ak.
·
Si A es triangular (superior o
inferior) entonces sus valores propios son los elementos diagonales.
Sean A y B dos matrices cuadradas. Se dice que A y B son semejantes si existe una matriz invertible T, tal que
A
= T B T-1 ó B=
T-1 A T
La relación de semejanza es una relación de equivalencia (cumple las
propiedades reflexiva, simétrica y transitiva).
Si
A y B son semejantes:
(i).
Tienen el mismo polinomio característico
(ii). Tienen los mismos valores propios con las mismas multiplicidades algebraicas.
·
Traza de una matriz
Sean A una matriz cuadrada. Se llama traza
de A a la suma de los elementos de la diagonal principal de A.
Si A y B son dos matrices semejantes cuadradas:
(i) det A = det B
(ii) rg A = rg B
(iii) tr A = tr B
·
Diagonalización
de matrices reales
Una matriz A cuadrada n´n es diagonalizable si es semejante a una matriz diagonal, D = T-1 A T.

Donde li
(i=1,...,n)
son los valores propios y vi
(i=1,...,n)
los vectores propios dispuestos en
columnas.
Si A es una matriz diagonalizable, entonces:
· Tiene n vectores propios linealmente independientes
· La suma de las dimensiones de los subespacios propios es n
· Si l0 es un valor propio de A de multiplicidad algebraica m 0, entonces
1 £ dim EA(l 0) £ m 0
·La multiplicidad algebraica de cada valor propio de A, coincide con la dimensión del subespacio propio correspondiente.
El
recíproco no tiene por qué ser cierto.

·
Diagonalización
de matrices reales simétricas
Las matrices simétricas siempre
se pueden diagonalizar. Poseen las siguientes características:
· Los
vectores propios asociados son ortogonales respecto al producto escalar canónico.
· Tiene
al menos un valor propio real.
· Toda
matriz simétrica es diagonalizable por una matriz
ortogonal:
D = Q-1 A Q = QT A Q
·
Matriz Ortogonal
Una matriz cuadrada será ortogonal si sus columnas son vectores ortonormales respecto al producto escalar canónico
QTQ
= I
·
Teorema espectral
Si una matriz A es una matriz simétrica,
entonces existe una base ortonormal de Ân
formada por los vectores propios de A.
Se llaman valores singulares de una matriz real A, cuadrada, a las raíces cuadradas positivas de los valores propios
de la matriz ATA. Notar que ATA es una matriz simétrica y
por ello diagonalizable.
Se llaman valores singulares de una matriz real A, no cuadrada, a las raíces cuadradas positivas de los valores
propios comunes de las matrices ATA y AAT.
1) Calcula los valores y vectores propios de las matrices siguientes:




Observa que es una matriz triangular
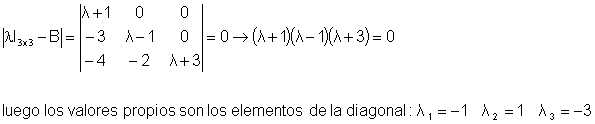
Vamos a hallar los vectores propios correspondientes a cada valor propio.



![]()
c).
 Observar que C es simétrica
Observar que C es simétrica

![]()


![]()



![]()
2) Indica cuáles de las matrices del ejercicio
anterior son diagonalizables y calcula la matriz diagonal en cada caso, así
como la matriz de paso.


![]()
3). Siendo a Î R, calcúlense los valores propios de la matriz:


Desarrollando por la primera fila:

Sacando factor común:
![]()

Aplicando la fórmula (a+b)(a-b)=a2-b2


·
Si ![]() , de la primera ecuación tenemos:
, de la primera ecuación tenemos:
![]()
y sustituyendo en la segunda ecuación:
![]()
![]() ,
con lo que
,
con lo que ![]()
La tercera y cuarta ecuación son equivalentes, y si
Caso
1. ![]() tenemos que
tenemos que ![]()
![]()
Así pues, dim EA(2)={(0,0,-1,1)} y A no es diagonalizable
Caso
2. ![]()

![]()
![]()
·
Si ![]() , de la segunda ecuación tenemos:
, de la segunda ecuación tenemos:
![]()
y sustituyendo en la primera ecuación:
![]()
![]() , con lo que
, con lo que ![]()
Llegamos, como en el estudio
anterior:
Caso
1. ![]() tenemos que
tenemos que ![]()
![]()
Así pues,
dim
EA(2)=1
y A no es diagonalizable
Caso
2. ![]() CASO YA ESTUDIADO
CASO YA ESTUDIADO
·
Si ![]()

![]() ,
, ![]() ,
, ![]()
![]()
Así pues,
dim
EA(2)=1
y A no es diagonalizable
Si ![]()

![]() ,
, ![]() ,
, ![]()
![]()
Así pues, dim
EA(2)=1
yA no es diagonalizable
Resumiendo, para el valor propio 2, la matriz únicamente
es diagonalizable si a
=
1.

·
Si ![]() , la primera y segunda ecuación
son equivalentes:
, la primera y segunda ecuación
son equivalentes:
![]()
y si sumamos la tercera
y la cuarta ![]()

Así pues,
dim
EA(3)=1
y A no es diagonalizable
·
Si ![]() ,
,

Por tanto
A es diagonalizable.
Resumiendo, para el valor propio 3, la matriz únicamente
es diagonalizable si a
=
0.