·  7.5. Estudio de los máximos y mínimos relativos de una función

         Los puntos c en los que   se denominan puntos críticos o puntos singulares.  Para saber si se trata de un máximo o mínimo relativo o de un punto de inflexión de tangente horizontal se puede emplear uno de estos métodos:

Método 1 

Estudiar la variación de la función en un entorno de  c:

        Si     f  máximo relativo en  c

        Si     f  mínimo relativo en  c

        En caso contrario  Þ  f  punto de inflexión de tangente horizontal en c

(Este método no nos parece el más conveniente y, por tanto, no lo utilizaremos en los ejemplos posteriores)

Método 2 

Estudiar la variación del signo de la derivada primera en un en­torno de c.  O sea, estudiar si  f  pasa de creciente a decreciente o viceversa al pasar de la izquierda a la derecha de c:

Si  pasa de positiva  a negativa    Þ  f  pasa de creciente en a decreciente en   Þ  f  máximo relativo en c

Si  pasa de negativa  a positiva    Þ  f  pasa de decreciente en a creciente en  Þ  f  mínimo relativo en c

Si  no cambia de signo a ambos lados de c  Þ  f  punto de inflexión de tangente horizontal en c.

Método 3

Estudiar el signo de la derivada segunda en esos puntos críticos  c,  pues

         si     f máximo relativo en c

         si     f mínimo relativo en c

         si     caso dudoso

como vamos a demostrar sucintamente:

¨  Se supone f definida y derivable en  y  f’  derivable en

         Si    siendo     y  f’  estrictamente decreciente en  c   Þ     y    y   Þ  f  tangente horizontal en  c  y  f  creciente en   y  f  decreciente en    Þ

 f  máximo en  c.

         Si    siendo   y  estrictamente creciente en  c  Þ     y    y    Þ   f  tangente horizontal en  c  y  f  decreciente en    y  f  creciente en    Þ

 f  mínimo en c.

         Si   y    Þ   caso dudoso. x

Ejemplos:

   a)  Sea

         En primer lugar utilizaremos el que hemos llamado “método 2”, al cual en realidad ya habíamos aludido implícitamente en el apartado anterior, pues es el que nos permite estudiar conjuntamente los intervalos de crecimiento y de decrecimiento y los máximos y mínimos relativos.

         Lo primero que haremos, pues, será hallar la derivada primera

 . Seguidamente la igualaremos a cero y resolveremos la ecuación resultante:

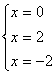            ®      ®     (puntos críticos)

         Teniendo en cuenta que el dominio de la función derivada f’ es ℝ, por ser polinómica, los únicos puntos que “separan” intervalos son los tres puntos críticos obtenidos.

Por tanto, hay que estudiar el signo de esa derivada primera f’ en ca­da uno de los cuatro intervalos en que ha quedado dividida la recta real y, para ello, el procedimiento práctico que se suele utilizar es el de darle a  x en cada caso un valor interior a ese intervalo:

De esta forma, pues, como se ha visto, hemos hallado a la vez los intervalos de crecimiento y de decrecimiento y los máximos y mínimos relativos de la función. Obsérvese que, para abreviar se ha escrito máximo y mínimo por máximo relativo y mínimo relativo respectivamente.

         Ahora utilizaremos el que hemos llamado “método 3”, para el cual también tendríamos que comenzar hallando la primera derivada, igualarla a cero y resolver la ecuación resultante para hallar los puntos críticos. Pero en este caso ese proceso ya lo hemos seguido antes, obteniendo como puntos críticos  –2,  0  y  2. Entonces lo único que nos queda ahora por hacer es hallar la función derivada segunda y “preguntarle” qué es cada uno de estos puntos “candidatos” a máximos o mínimos. Tendremos, pues,

Por lo que:

           Þ  f  mínimo relativo en

           Þ  f  máximo relativo en

           Þ  f  mínimo relativo en

como ya habíamos obtenido por el otro método.

         Al comparar ambos métodos el alumno observará que, si bien el primero de ellos es más largo y trabajoso, también proporciona a cambio mayor información sobre la función. El segundo, en cambio, es algo más breve, pero sólo nos indica los máximos y los mínimos relativos.

   b)  Sea ahora  

         Por el primer procedimiento tendremos 

  e igualando a cero

           ®    ®    ®    ó 

                                                                               (puntos críticos)

         Pero el dominio de la derivada primera   es ℝ∼. Luego los puntos que “separan” intervalos son 0, 1  y  2. Estudiando el signo de f’  en esos intervalos tendremos:

Por el segundo procedimiento, una vez hallados los puntos críticos, 0  y  2, hallaríamos la derivada segunda y estudiaríamos el signo de la misma en dichos puntos:

Pero al llegar aquí hemos de hacer una importantísima advertencia al alumno. Y es que se ha de fijar bien que en las derivadas segunda, tercera, etc. de las funciones racionales siempre deberá simplificar la fracción antes de “lanzarse” a hacer operaciones que complicarían el ejercicio inútilmente.

En el caso que nos ocupa, hemos de fijarnos en que en el numerador hay dos términos y en ambos está repetido el factor  que aparece en el denominador. Por tanto, en virtud de la propiedad distributiva de la división respecto a la resta, se podrá simplificar numerador y denominador, dividiéndolos aquí por , y quedando:

Entonces:

                     Þ  f  máximo en

                      Þ   f  mínimo en