·  7.6. Concavidad y convexidad de una función

Sea  f  definida y derivable en    y sea 

Definiciones

         f  cóncava en  c hacia las Y positivas   Û    creciente en  c

        f  convexa en  c  hacia las Y positivas    Û    decreciente en  c

·  7.7. Condiciones suficientes de concavidad y convexidad

Teorema:  Sea  f  definida y derivable en   ,  siendo    derivable a su vez en 

         si   f  cóncava en  c

         si   f  convexa en  c

¨  Evidentemente

             creciente en  c  Û  f  cóncava en  c

         Þ    decreciente en  c  Û  f  convexa en  c   x

Definición

  f  cóncava (convexa) en    Û  f  cóncava (convexa) en  x ,

·  7.8. Estudio de los intervalos de concavidad y convexidad de una función

         Se estudia el signo de  en los intervalos que las raíces de la ecuación    determinan sobre el dominio de  .

         Antes de aplicar este método a algún ejemplo concreto, preferimos actuar como en el caso de los intervalos de crecimiento y de decrecimiento, dejándolo para utilizarlo después de haber estudiado los puntos de inflexión en el apartado siguiente.

·  7.9. Puntos de inflexión

Definición: f  tiene un punto de inflexión en  c  Û  f  pasa en  c de cóncava a convexa o viceversa.

·  7.10. Condiciones suficientes de punto de inflexión

 Sea  f  definida y derivable en    siendo   y   derivables a su vez en 

          y    Þ   f  punto de inflexión en  c

¨    

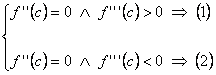
y f’’ creciente en cy y  Þ

     derivable en c y f convexa en   y f cóncava en    Þ

     punto de inflexión en c.

y f’’ decreciente en cy yÞ

      derivable en  c y f  cóncava en   y f  convexa en    Þ

       punto de inflexión en c.x