· 7.11. Estudio de los puntos de inflexión de una función
Se hallan las raíces de la ecuación
![]() , que son los posibles puntos de inflexión. Después, para
averiguar si lo son o no, se puede recurrir al estudio de los intervalos de
concavidad y convexidad, o bien a la condición suficiente. Si se aplica este
último método puede darse el caso dudoso
, que son los posibles puntos de inflexión. Después, para
averiguar si lo son o no, se puede recurrir al estudio de los intervalos de
concavidad y convexidad, o bien a la condición suficiente. Si se aplica este
último método puede darse el caso dudoso
![]() y
y ![]() .
.
Ejemplos:
a) Retomemos la función
![]() , cuyos intervalos de crecimiento y de decrecimiento y sus
máximos y mínimos relativos ya estudiamos en los apartados anteriores. Ahora se
trata de estudiar los intervalos de concavidad y convexidad y los puntos de
inflexión.
, cuyos intervalos de crecimiento y de decrecimiento y sus
máximos y mínimos relativos ya estudiamos en los apartados anteriores. Ahora se
trata de estudiar los intervalos de concavidad y convexidad y los puntos de
inflexión.
Si elegimos el primero de los caminos,
partiremos de la segunda derivada, que ya teníamos hallada,
![]() , e, igualándola a cero, resolveremos la ecuación
correspondiente:
, e, igualándola a cero, resolveremos la ecuación
correspondiente:
![]() ®
®
![]() ®
®
![]() (posibles puntos de inflexión)
(posibles puntos de inflexión)
Como el dominio de esta derivada segunda es ℝ, por ser polinómica, habrá que estudiar el signo de f’’ en los siguientes intervalos:
Si elegimos el segundo camino, después
de obtener los posibles puntos de inflexión,
![]() y
y ![]() , hallaremos la derivada tercera a la cual “preguntaremos” si
realmente estos puntos son de inflexión.
, hallaremos la derivada tercera a la cual “preguntaremos” si
realmente estos puntos son de inflexión.
![]()
Por tanto,
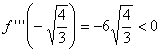 Þ f punto de inflexión en
Þ f punto de inflexión en
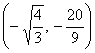
 Þ
f punto de inflexión en
Þ
f punto de inflexión en 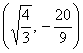
En ambos casos
![]() se ha obtenido sustituyendo x por
se ha obtenido sustituyendo x por
![]() en
en ![]() .
.
b) Retomemos ahora el segundo ejemplo del apartado anterior, es decir,
![]()
Como ya teníamos hallada la derivada segunda
![]() , sólo tendremos que igualarla a cero y resolver la ecuación
obtenida. Pero en este caso
, sólo tendremos que igualarla a cero y resolver la ecuación
obtenida. Pero en este caso
![]() no tiene solución, ya que sólo el numerador habría de ser
0
no tiene solución, ya que sólo el numerador habría de ser
0
Por tanto, esta función no tendrá puntos de inflexión.
c) Como el anterior ejemplo de función racional no ha tenido puntos de inflexión, quisiéramos añadir uno más que sí los tenga.
Sea
![]() . Su derivada primera será
. Su derivada primera será
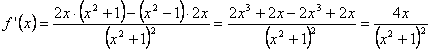
Y su derivada segunda:
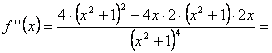 y, sin olvidar simplificar,
y, sin olvidar simplificar,

Igualándola a cero, tenemos la ecuación
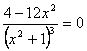 ®
®
![]() ®
®
![]() ®
®
![]() que son
que son
los posibles puntos de inflexión. Como el dominio de f’’ es ℝ puesto que su denominador no se anula por ser una suma de cuadrados (elevada al cubo), sólo hemos de estudiar el signo de f’’ en los siguientes intervalos:
Todo ello si elegimos el primer procedimiento. Si hubiéramos optado por el segundo, una vez hallados los posibles puntos de inflexión, habremos de hallar la derivada tercera que será
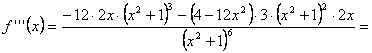 ¡simplificando!
¡simplificando!
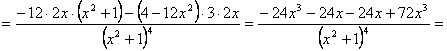
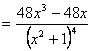
Y sustituyendo en ella los posibles puntos de inflexión:
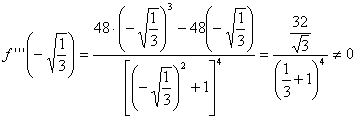 Þ f punto de inflexión en el punto
Þ f punto de inflexión en el punto
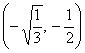 , donde
, donde 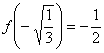 .
.
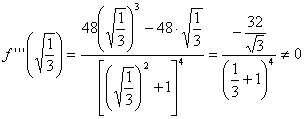 Þ
f punto de inflexión en el punto
Þ
f punto de inflexión en el punto
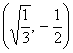 , donde
, donde 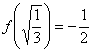
como habíamos hallado por el proceso anterior.
El alumno habrá sin duda observado que los cálculos con las derivadas segunda y tercera pueden hacerse a veces un poco “largos”, pero la práctica le ha de ser, indudablemente, de gran utilidad.
|
|